Seit einer Woche nehmen sich einige Medien der Wirren um die Wirksamkeit von Impfstoffen an. So titelt etwa FOCUS „Viele Mediziner verstehen grundlegende Statistiken nicht“. FOCUS leider auch nicht – oder zumindest nennt man den Elefanten, der da dick und breit im Raum steht, nicht beim Namen: Eigentlich sagt die Wirksamkeit nichts aus.
Lesen Sie weiter →Was die Welt im Innersten zusammenhält
Ein wissenschaftlicher Blog über die verblüffenden Zusammenhänge der Welt
Schlagwort: Statistik (page 1 of 2)
In der Mathematik kann man durch Wechsel der Perspektive mitunter sehr hilfreiche Formeln ans Tageslicht befördern. Für den Erwartungswert einer Zufallsvariable X gilt im diskreten Fall:
Und im kontinuierlichen Fall gilt:
Dieser Beitrag erklärt, wie sich diese Formeln herleiten lassen.
Lesen Sie weiter →Eine der Sachen, die ich nie so richtig nachvollziehen konnte, ist die Beziehung der Chi-Quadrat-Verteilung zur Stichprobenarianz. Diese Beziehung nutzt man beispielsweise, um bei vorliegender Stichprobenvarianz einer normalverteilten Grundgesamtheit auf die Varianz der Population zu schließen. Wir sprechen also über eines der wichtigeren Kapitel der Statistik. Lesen Sie weiter →
Vor vielen Jahren, als ich noch am Anfang meiner dienstlichen Laufbahn stand, überzeugte mich meine Versicherungsmaklerin von einer Riester-Rente. Im Lauf der Jahre stellte ich mir doch immer wieder die Frage, ob beim Produkt „Index Select“ der Allianz alles mit rechten Dingen zugeht. Tatsächlich beschlich mich das Gefühl, bei der Wahl zwischen sicherer Verzinsung und Index-Partizipation immer daneben zu greifen. Eine Analyse der Mechanismen und Daten der Vergangenheit werden im Rahmen dieses Beitrags Licht ins Dunkel bringen. Aber gehen wir erstmal einen Schritt zurück zum Produkt selbst.
Lesen Sie weiter →
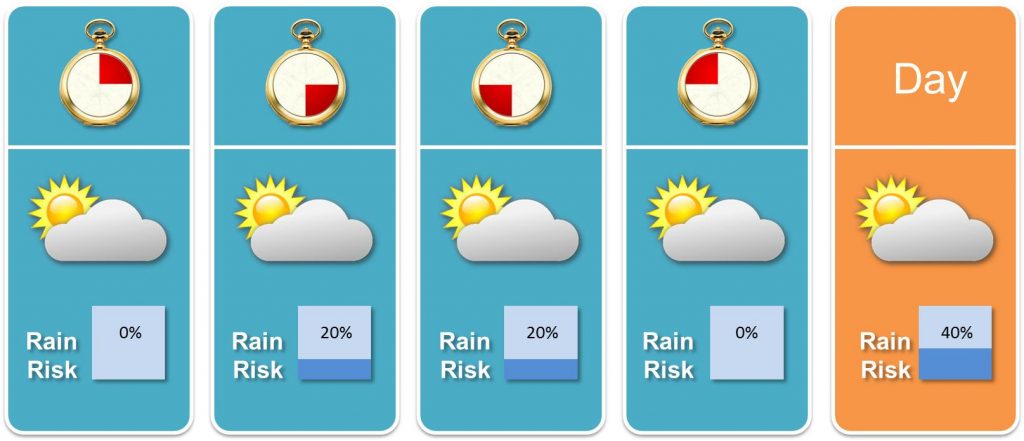
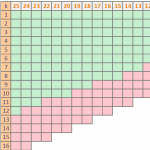
Es geht wieder in großen Schritten auf die dunkle Jahreszeit zu – und Stück für Stück steigt das Regenrisiko. Wer empfindliche Kleidung tragen will, schaut daher lieber in den Wetterbericht. Dabei wird der eine oder andere sicher bereits festgestellt haben, dass die Niederschlagswahrscheinlichkeit inzwischen sehr detailliert (bis auf die Stunde genau) angegeben wird. Bedeutung und Zusammenhang zwischen der groben täglichen Niederschlagswahrscheinlichkeit und ihren feineren Abstufungen geben dabei vielen Mitmenschen Rätsel auf. Nehmen wir folgendes Beispiel vom Schwesternblog Insight Things her:
Was sagt uns das Regenrisiko/Niederschlagswahrscheinlichkeit ganz generell? Und wie kommt man von 2 mal 20% Regenwahrscheinlichkeit auf 40% für den ganzen Tag? Diese Fragen werde ich im Folgenden beantworten!
In meinen früheren Beiträgen habe ich bereits über Addieren und Multiplizieren von Mittel- und Erwartungswerten berichtet. Was das Dividieren angeht, möchte ich jedoch etwas zur Vorsicht mahnen. Man muss genau schauen, ob tatsächlich der Kehrwert vom Mittelwert gemeint ist!
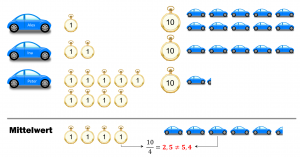
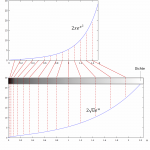
Man bedenke folgendes Beispiel: Alex behält seine Autos in der Regel für ein Jahr, Ina zwei Jahre und Peter 9 Jahre. Im Mittel behalten sie die Autos also 4 Jahre. Heißt das nun, dass die drei Personen im Durchschnitt 10/4=2,5 Autos pro 10 Jahre besitzen? Sehen wir uns die Sache anhand des Bildes unten genauer an.
Zum Überschlagen von Erwartungswerten kann es hilfreich sein, wenn man Erwartungswerte multipliziert. Dieser Beitrag zeigt, dass es legitim ist Erwartungswerte zu multiplizieren, wenn es sich – anders als beim Addieren von Erwartungswerten – um Erwartungswerte unabhängiger Zufallsvariablen handelt. Da Mittelwerte Schätzer von Erwartungswerten sind, gelten die Ausführungen auch für Mittelwerte. Lesen Sie weiter →
Es handelt sich zwar um einen sehr intuitiven Aspekt der Statistik, der Vollständigkeit wegen sollte er aber nicht unerwähnt bleiben: Warum man Erwartungswerte addieren darf. Da Mittelwerte Schätzer von Erwartungswerten sind, gelten die Ausführungen auch für Mittelwerte. Lesen Sie weiter →
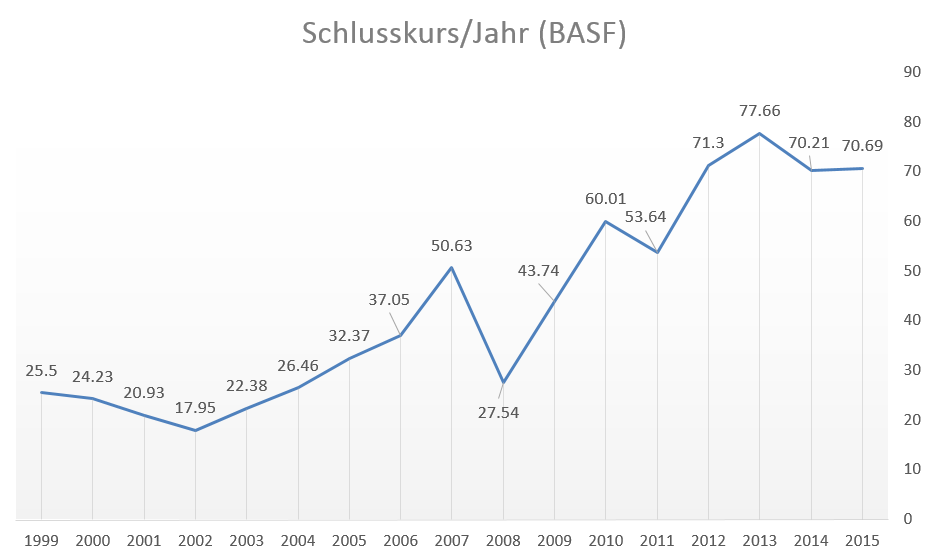
Wahrsager haben ihr Kristallkugeln und Wissenschaftler ihre Modelle. Für fundierte Prognosen an der Börse stellen statistische Modelle sicher das probatere Mittel dar. Dieser Beitrag zeigt am Beispiel der BASF-Aktie wie man auf Basis historischer Daten eine Vorhersage für die diskrete Rendite über die nächsten 5 Jahre treffen kann. Ganz nebenbei werden wir sehen, dass Renditen theoretisch immer derselben Verteilungsfamilie folgen (was eine der Grundannahmen des Black-Scholes-Modells darstellt). Untermauert werden alle Schritte durch entsprechende Simulationen, die ihr mittels R-Skript sowie jahres- und tagesfeinen Daten nachvollziehen könnt!
In ihrem Beitrag „Warum es keine 140jährigen Menschen gibt“ beschreibt die sympathische Autorin, weshalb die Wahrscheinlichkeit sehr gering ist, dass ein Mensch in die Alterssphären von 110, 120 oder gar 130 Jahren vordringt. Demnach erreichen beispielsweise von tausend 100jährigen gerade einmal 6 ein Alter von 110. Die Rechnung ist durchdacht und hinsichtlich ihrer Schlüsse kann ich der Autorin in weiten Teilen reinen Gewissens folgen. Nichtsdestotrotz erscheinen einige Zwischenergebnisse unter Berücksichtigung von Wahrscheinlichkeitsverteilungen in einem ganz anderen Licht – wie ich zeigen werde! Lesen Sie weiter →
© 2024 Was die Welt im Innersten zusammenhält
Theme by Anders Noren — Up ↑