Statistisch modelliert: So sind Renditen verteilt!

Inhalt

Verwendete Daten
Simulation der Rendite
Herleitung der Renditeverteilung
Schlussfolgerungen

Wahrsager haben ihr Kristallkugeln und Wissenschaftler ihre Modelle. Für fundierte Prognosen an der Börse stellen statistische Modelle sicher das probatere Mittel dar. Dieser Beitrag zeigt am Beispiel der BASF-Aktie wie man auf Basis historischer Daten eine Vorhersage für die diskrete Rendite über die nächsten 5 Jahre treffen kann. Ganz nebenbei werden wir sehen, dass Renditen theoretisch immer derselben Verteilungsfamilie folgen (was eine der Grundannahmen des Black-Scholes-Modells darstellt). Untermauert werden alle Schritte durch entsprechende Simulationen, die ihr mittels R-Skript sowie jahres- und tagesfeinen Daten nachvollziehen könnt!

Kursentwicklung der BASF-Aktie zwischen 1999 und 2015

Verwendete Daten

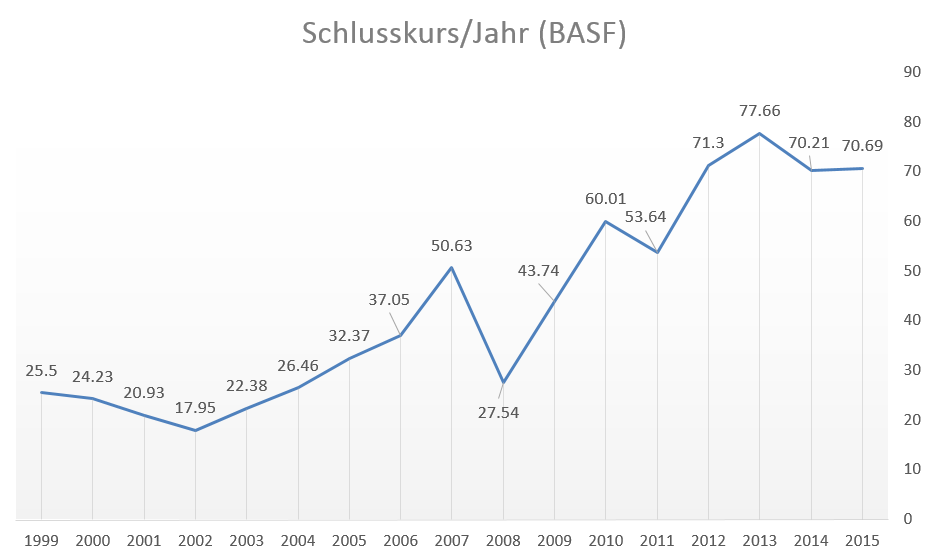
Ich haben die historischen Daten der BASF-Aktie an der Frankfurter Börse über finanzen.net abgerufen. Auf Basis der Schlusskurse eines jeden Jahres von 1998 bis 2015 ergeben sich die jährlichen diskreten Renditen. Die Renditedaten könnt ihr euch hier hier herunterladen.

Histogramm der Renditen pro Jahr

Die jährlichen Renditen werden später als Näherung der Renditeverteilung verwendet. Es sind nur die Kursveränderungen eingeflossen; Dividenden gehören hier in der Praxis aber ebenfalls hinein. Für unsere theoretischen Betrachtungen sind wir damit dennoch gut aufgestellt 😉

Simulation der Rendite

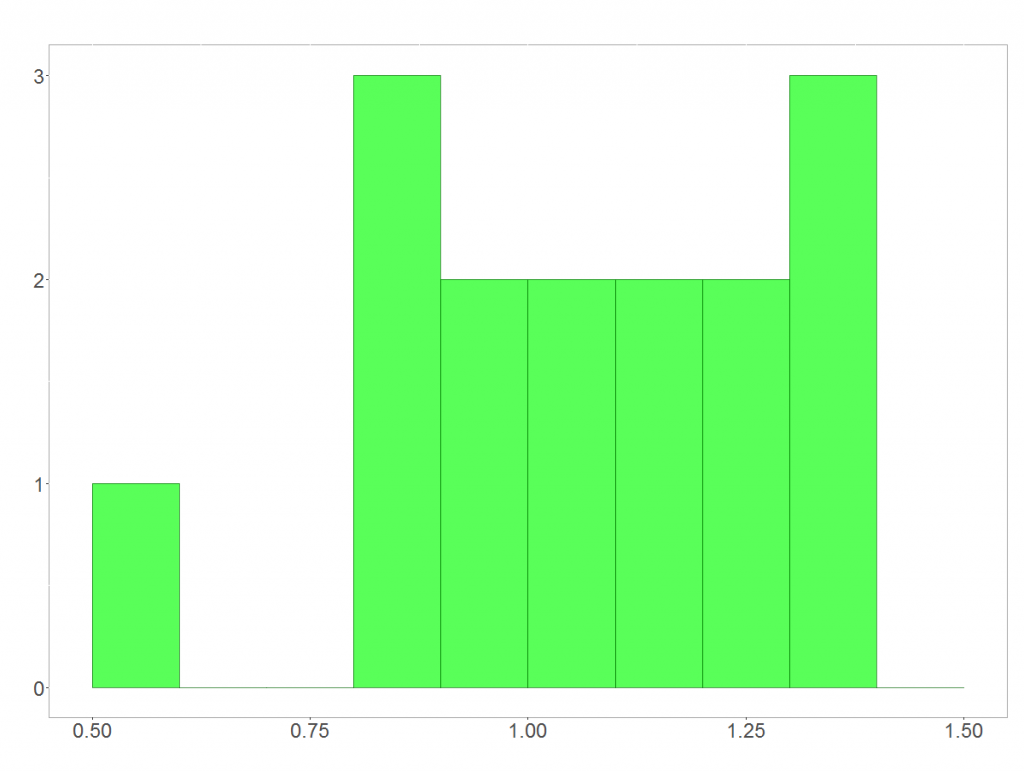
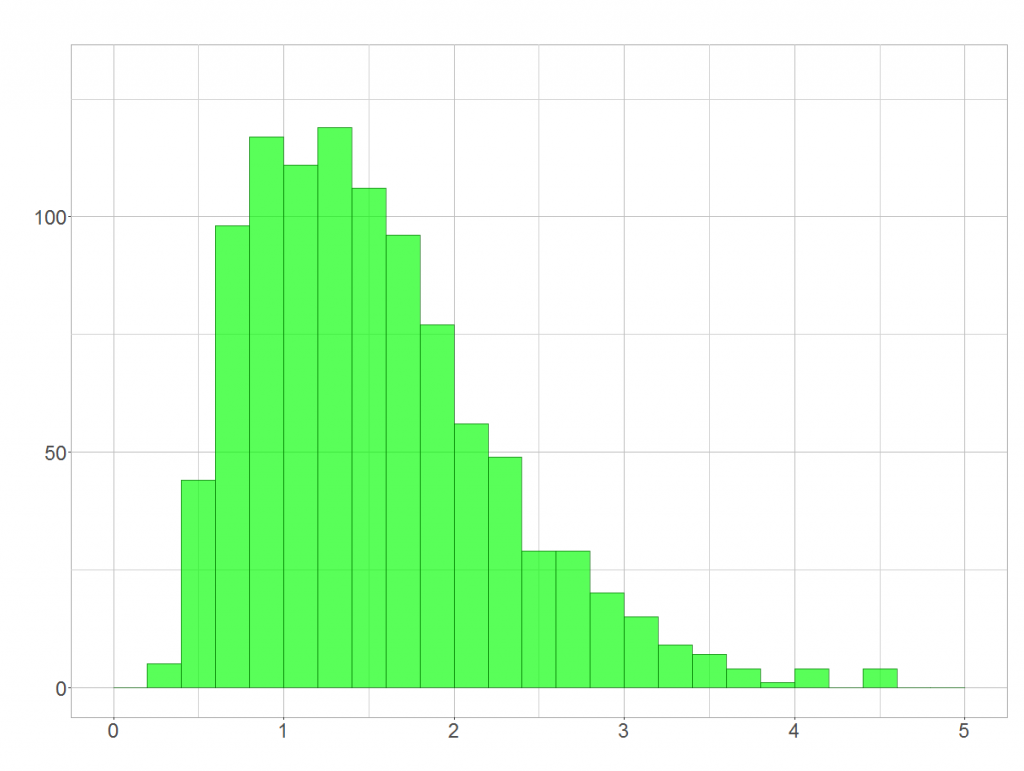
Zunächst werden wir uns der 5-Jahres-Prognose über eine Simulation nähern. Dazu stellen wir uns vor, dass die jährlichen Renditen unsere tatsächliche Renditeverteilung darstellen. Wenn wir zufällig fünf Werte aus dieser Verteilung ziehen und multiplizieren, stellt dies jeweils einen plausiblen Wert für die Rendite über 5 Jahre dar. Wiederholen wir dies oft genug, bekommen wir mittels Häufigkeitsverteilung einen guten Eindruck davon, wie wahrscheinlich bestimmte Renditen über 5 Jahre sind. Ich habe dies in R 1000 Mal durchgeführt:

Histogramm der multiplizierten Stichproben vom Umfang 5

Wenn das mal nicht nach einer logarithmischen Normalverteilung (Log-Normalverteilung) aussieht! Es ist übrigens so, dass man bei dieser Simulation ganz unabhängig von den Grunddaten immer auf eine Log-Normalverteilung stößt. Warum das so ist, zeige ich euch gleich!

Herleitung der Renditeverteilung

Mathematisch kann man das Phänomen der logarithmisch normalverteilten Renditen relativ einfach nachweisen. Zunächst bezeichnen wir zufällig gezogene jährliche Renditen als Zufallsvariablen $R_{i}$ . Für einen Zeitraum von $n$ Jahren ergibt sich die zufallsverteilte, prognostizierte Rendite $R_{P}$ zu:

$\displaystyle R_{P}=R_{1} \cdot R_{2} \cdot R_{3} \cdot \dots \cdot R_{n}=\prod\limits_{i=1}^{n} R_{i}$

Logarithmieren wir nun beide Seiten der Gleichung. Statt eines Produktes erhalten wir eine Summe.

$\displaystyle \ln(R_{P})=\ln\Big(\prod\limits_{i=1}^{n} R_{i}\Big)=\ln(R_{1})+\ln(R_{2})+\ln(R_{3})+\dots+R_{n}=\sum\limits_{i=1}^{n} \ln(R_{i})$

Das entspricht in etwa der Situation, wenn man die gezogenen Werte logarithmiert und dann addiert. Stellen wir uns vor, dass wir aus Daten ziehen, die von vornherein logarithmiert sind und geben den Zufallsvariablen die Namen $L_{i}$ .

$\displaystyle \ln(R_{P})=\sum\limits_{i=1}^{n} \ln(R_{i})=\sum\limits_{i=1}^{n} L_{i} \approx R^{*}$

$\displaystyle R^{*} \sim \mathcal{N}\Big(n \cdot E[L], \, n \cdot Var[L]\Big)$

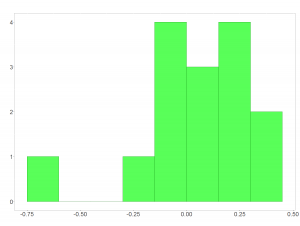
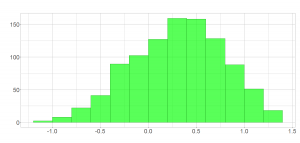
Wie wir sehen führt die Addition mehrerer (unabhängiger!) Zufallsvariablen zu einer Normalverteilung. Begründet werden kann dies mit dem zentralen Grenzwertsatz. Wer davon zum ersten Mal hört, wird es vielleicht nicht glauben können. Daher zeigt das erste Bild unten unsere Renditedaten in logarithmierter Form. In R habe ich wiederrum simuliert, was passiert, wenn man 1000 Stichproben zieht und jeweils addiert. Das Ergebnis seht ihr im zweiten Bild; trotz sehr dünner Datenlage lässt sich problemlos eine Normalverteilung interpretieren.

Histogramm der logarithmierten Renditen

Normalverteilung nach Stichproben aus logarithmierten Renditen

Nun exponenzieren wir nochmals, um an unsere Prognoseverteilung $R_{P}$ zu gelangen:

$\displaystyle e^{\ln(R_{P})}=e^{ R^{*}}$

$\displaystyle R_{P}=e^{R^{*}}$

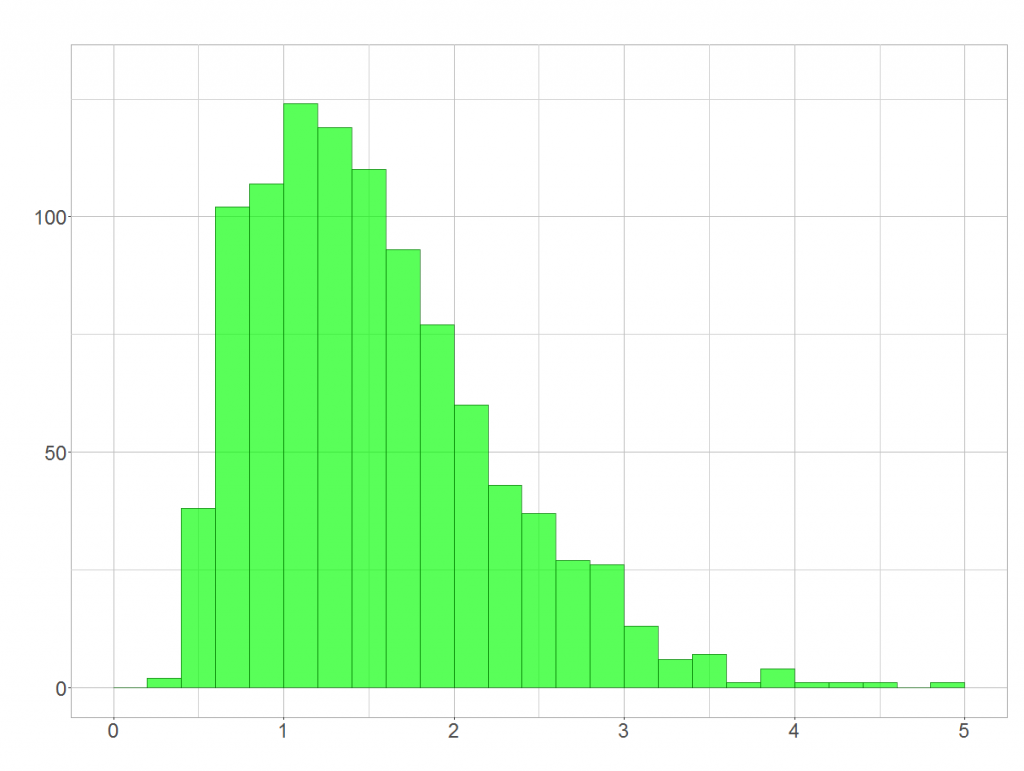
Das ist jetzt aber eindeutig die Definition der logarithmischen Normalverteilung 😉 Wir können das auch wieder durch Simulation zeigen. Exponenzieren wir die Werte aus der Normalverteilung von oben, zeigt sich das erwartete Bild:

Histogramm der exponenzierten Normalverteilung

Schlussfolgerungen

Was können wir damit anstellen? Zum Beispiel können wir die Wahrscheinlichkeit, in den nächsten 5 Jahren Geld zu verlieren, mit ca. 29,1% angeben. Wie man dererlei Sachen unter Nutzung der logarithmierten Rendite berechnet, werde ich aber nochmal in einem separaten Beitrag beschreiben.

Die wichtigste Schlussfolgerung: Unter der Annahme unabhängiger Handelsintervalle stellt sich offenbar eine Log-Normalverteilung für die diskrete Rendite ein! In der Praxis sind Handelsintervalle allerdings nicht vollkommen unabhängig, da beispielsweise ein große Transaktion den Kurs einer Aktie beeinflussen und weitere Verkäufe nach sich ziehen kann. Dies erklärt, warum reale Rendiedaten sich stärker um den Mittelwert drängen, aber auch weiter in die Randbereiche auslaufen können. Für uns Otto-Normalverbraucher ist die Log-Normalverteilung jedoch bereits sehr genau.

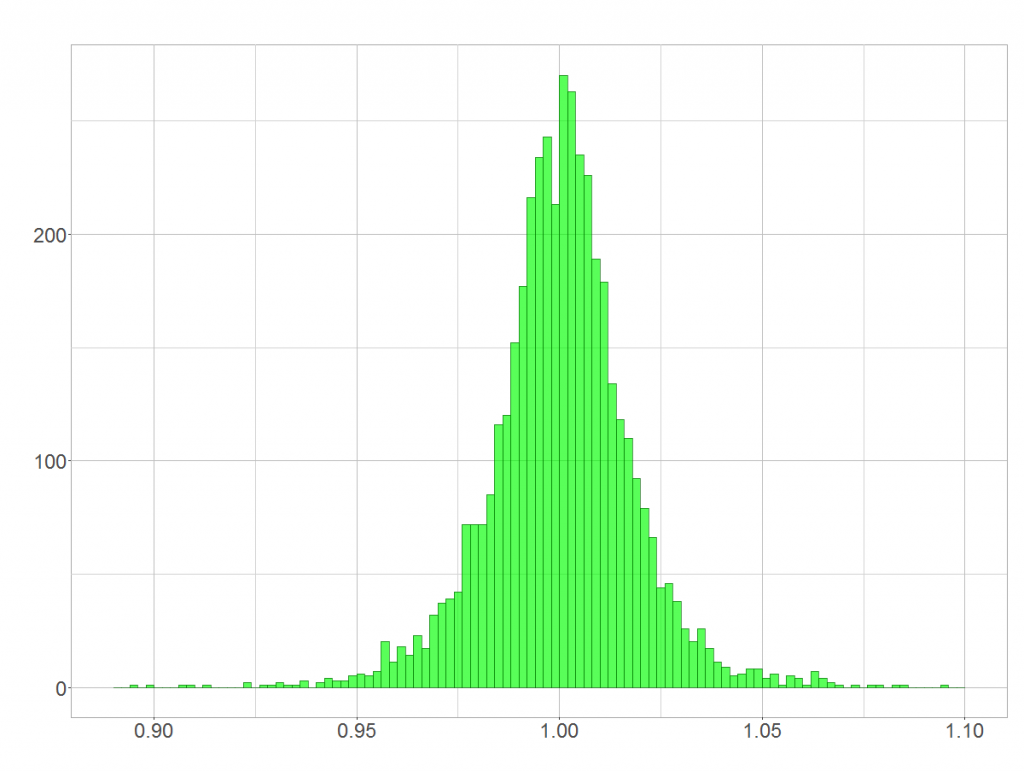
Nun ist ja nicht nur ein 5-Jahres-Zeitraum aus Jahren aufgebaut. Auch ein Jahr besteht wiederum aus Tagen, sodass wir davon ausgehen können, dass auch Jahresrenditen in etwa logarithmisch normalverteilt sind. Und die Tage bestehen aus Stunden und Minuten, sodass tagefeine Renditen ebenfalls logarithmisch normalverteilt sein sollten. Da an einem Tag alleine nicht viel passiert, zentrieren sich die Werte um eine Rendite von 1. Die Verteilung (ihr könnt die tagesfeinen Daten hier abrufen) ist sehr symmetrisch, was aber kein Widerspruch ist. Ich habe das Thema in meinem Beitrag (Irreführendes) Erscheinungsbild der Log-Normalverteilung aufgefriffen.