Eine der bekanntesten Verteilungen der Statistik ist die Normalverteilung. Und weil sie so bekannt ist, sind auch relativ viele Menschen schnell dabei, Sachverhalte als normalverteilt hinzunehmen. Oftmals kann aber die Log-Normalverteilung – sozusagen der kleine Bruder der Normalverteilung – das passendere Modell sein! Prominente Beispiele für logarithmisch normalverteilte Daten sind wichtige Themen wie Spritverbräuche und Renditen. In diesem Beitrag soll es darum gehen, dass man den Unterschied zwischen der Normalverteilung und der Log-Normalverteilung manchmal nicht auf den ersten Blick sieht.
Transformation zwischen Normalverteilung und Log-Normalverteilung
Eine Normalverteilung entsteht immer dort, wo eine genügend große Anzahl von Zufallsgrößen additiv verknüpft ist, während die Log-Normalverteilung durch die multiplikative Verknüpfung entsteht. Seien und
beliebige Zufallsvariablen, dann ist
normalverteilt und
logarithmisch normalverteilt:
Der Zusammenhang zwischen Normal- und Lognormalverteilung kann gezeigt werden für den Fall, dass
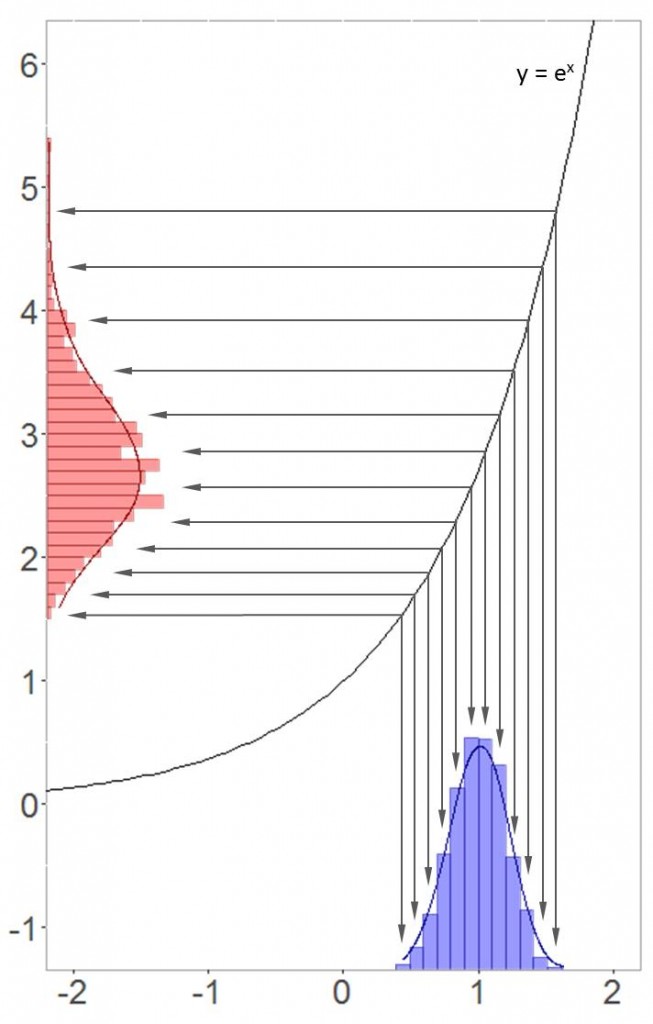
Diese Transformation zwischen beiden Verteilungen kann man grafisch darstellen. Dazu habe ich in R 1000 um 1 normalverteilte Werte generieren lassen. Wenn wie nun jeden Wert der Normalverteilung auf der x-Achse exponenzieren, erhalten wir die Log-Normalverteilung auf der y-Achse.
Durch den steiler werdenden Ansteig der e-Funktion werden die größeren Werte stärker gestreckt – deshalb ist die Log-Normalverteilung auch positiv schief. Doch nicht immer nimmt die Log-Normalverteilung diese typische Form an, wie wir am Beispiel von Renditen sehen werden!
Diskrete Rendite: Normal- oder Log-Normalverteilung?
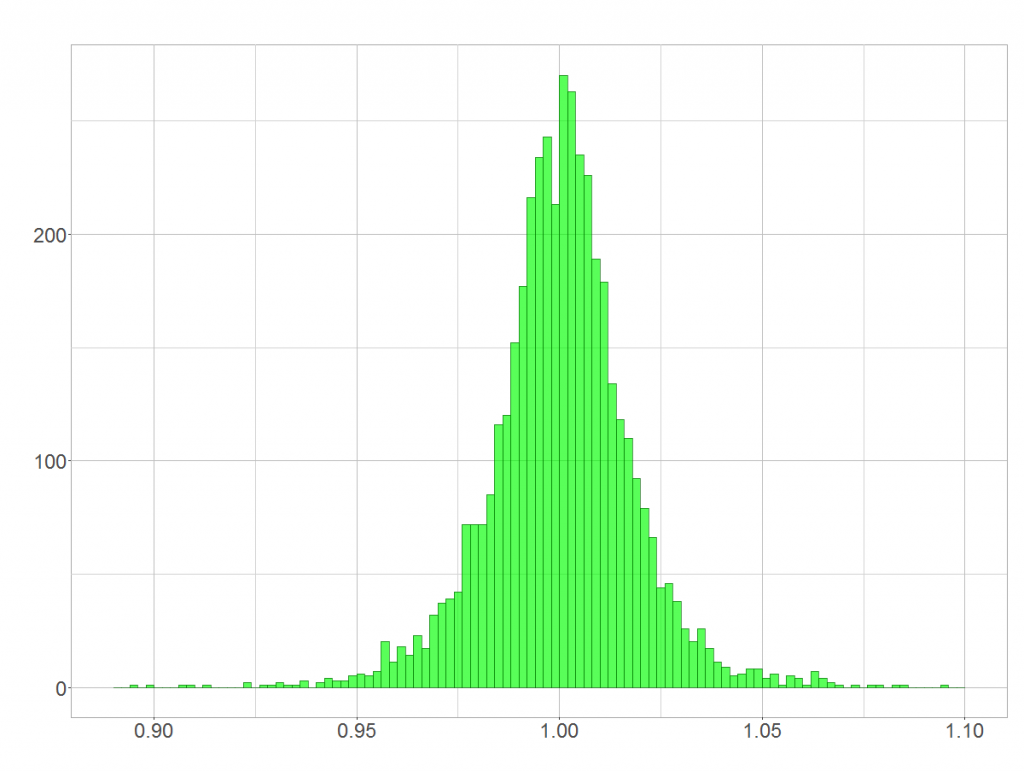
Kleine Preisfrage zu Beginn: Sind die tagesfeinen Renditen der BASF-Aktie, welche unten dargestellt sind, normalverteilt oder folgen sie einer Log-Normalverteilung?
Allein optisch kann man es aus diesem Histogramm nicht erkennen. Wer aber meinen Beitrag „Statistisch modelliert: So sind Renditen verteilt!“ gelesen hat, weiß um die theoretischen Hintergründe. Tatsächlich sind diskrete Renditen logarithmisch normalverteilt. Aber wie kommt es zur oben gezeigten Verteilung, die doch scheinbar besser zu einer Normalverteilung passt?
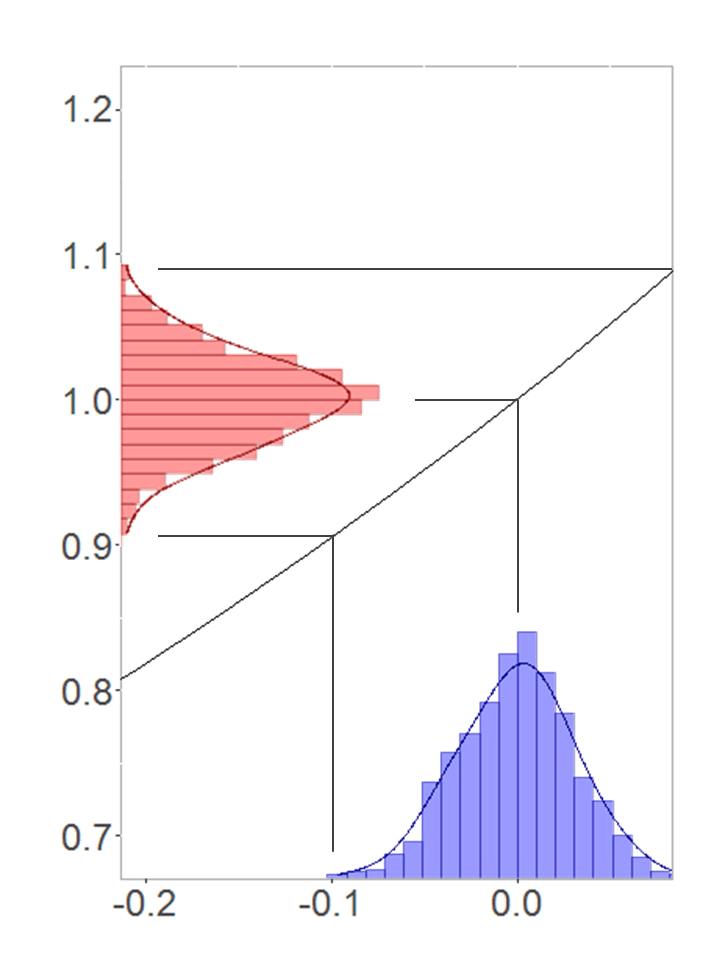
Dazu habe ich wieder 1000 Werte aus einer Normalverteilung gezogen, welche mit geringer Varianz um 0 streuen. Die Transformation sieht nun wie folgt aus.
Hier kommen zwei Faktoren zusammen: Einerseits können wir die e-Funktion wegen des kleinen Intervalls, auf dem die Transformation stattfindet, durch eine Gerade approximieren. Außerdem hat diese Gerade den Anstieg 1, weil die e-Funktion an der Stelle 0 ebenfalls den Anstieg 1 aufweist. Dies führt nahezu zu einer 1:1-Transformation der Verteilungen und damit auch zu einer sehr ähnlichen Symmetrie. Übrigens funktioniert das auch ähnlich, wenn die zugrundeliegende Normalverteilung um höhere Werte als 0 streut – die Standardabweichung der Normalverteilung muss dann nur deutlich kleiner werden.
Fazit
Abschließend möchte ich noch einmal den Leser dazu anhalten, lieber zweimal über die Wahl des richtigen Verteilungsmodells nachzudenken. Die Gefahr besteht darin, dass man falsche Rückschlüsse zieht und verallgemeinert. Wenn sich also Peter die Verteilung der tagesfeinen Renditen anschaut und anschließend seinem Kumpel Thomas erzählt, dass Renditen normalverteilt sind, kann das Folgen haben. Thomas könnte nun auf die Idee kommen eine Regression über die Daten zu legen und dabei seltsame Ergebnisse erhalten – beispielsweise negative diskrete Renditen 😀

 (15 Stimmen, Durchnschnitt: 4,67 von 5)
(15 Stimmen, Durchnschnitt: 4,67 von 5)




26. August 2019 at 13:07
Nicht die sog. Normalverteilung ist „Normal“, sondern die Log-Normalverteilung ist in mindestens 95 von 100 Verteilung die richtige Verteilung. Beispiele Lagerverteilung die Verteilung von Kassenumsätzen etc.