Die gedrehte Münze

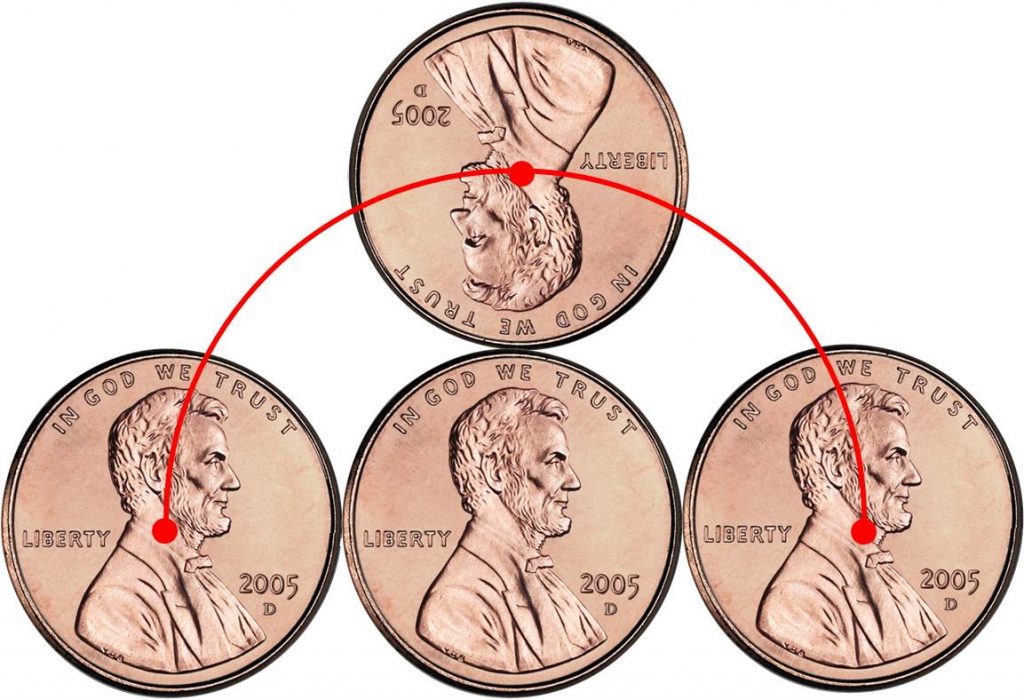
Ihr glaubt, dass euch schonmal ein Rätsel in die Irre geführt hat? Dann kennt ihr dieses hier noch nicht 😛 Ihr legt zwei gleiche Münzen flach auf den Tisch und dreht die eine um die andere (siehe Skizze). Was glaubt ihr: Wird Mr. Lincoln wieder aufrecht auf der anderen Seite ankommen oder steht er auf dem Kopf?

Steht die Münze nach der Drehung auf dem Kopf?

Lösung durch Ausprobieren

Die einfachste Art, sich der Lösung zu nähern, besteht im reinen Ausprobieren. Die Abbildung unten zeigt, dass die Münze nach dem Zurücklegen des Halbkreises eine ganze Rotation geschafft hat.

Die Rotation der Münze Schritt für Schritt

Dem ein oder anderen wird vielleicht aufgefallen sein, dass die Bewegung in der Tat aus zwei Komponenten besteht: Eine halbe Rotation um die zweite Münze und eine halbe „echte“ Eigenrotation. Wenn ihr die Münze herumschiebt und immer derselbe Punkt die zweite Münze berührt (Mr. Lincoln schaut also permanent auf sich selbst), dann erhaltet ihr die erste Hälfte der Rotation. Die zweite Hälfte ergibt sich aus dem Umstand, dass die Münze durch das Rollen ja auch eine halbe Drehung um sich selbst – relativ zur Bahn, auf der sie sich bewegt – vollführt.

Die elegante Lösung

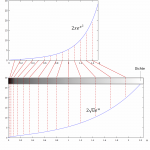
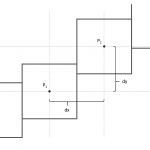
Die Rotation der bewegten Münze ergibt sich aus der Bewegung der Randpunkte. Der zurückgelegte Weg der einzelnen Punkte ist sowohl abhängig von der Entfernung zum Mittelpunkt der inneren Münze wie auch vom eigenen Radius. Fakt ist aber, dass die Radien immer linear eingehen. Die Idee ist nun, die radiale in eine lineare Bewegung zu überführen.

Die Entfernung, die der Mittelpunkt der bewegten Münze zurücklegt

Bezeichne den Radius der Münze, dann gilt für den zurückgelegten Weg des Münzenmittelpunktes:

Legt die Münze eine solche Entfernung auf der Geraden zurück, so dreht sie sich exakt einmal um sich selbst. Die volle Rotation als Lösung des Rätsels ist also gar nicht so spektakulär.

Der Mittelpunkt legt die gleiche Entfernung auf der geraden zurück