Inhalt
Heute geht es wieder um die großen Geheimnisse des Universums. In „Physik des Toilettenpapierspenders“ habe ich versucht, dem Mysterium unvermitteltem Klopapier-Reißens auf die Schliche zu kommen. Es stellte sich jedoch heraus, dass es neben der Bauform des Toilettenpapierhalters noch weitere Faktoren geben muss, welche Risswahrscheinlichkeit und -position beeinflussen. Dieser Beitrag führt die begonnene Forschung fort und untersucht die Verteilung der Kraft beim Ziehen am Toilettenpapier – entweder an einem Toilettenpapierspender mit Abrollbremse und/oder bei ruckartigem Ziehen an einer Toilettenpapierrolle ohne Abrollbremse.
Vorgehen
Wir werden uns drei Fällen ansehen. Der erste (und einfachste) Fall „Gleichmäßiges Ziehen“ wird die Grundlagen schaffen. Der zweite Fall „Gerades Ziehen in einem Punkt“ wird deutlich mathematischer angehaucht sein und könnte jenen Mitmenschen mit geringem Klopapier-Fetisch etwas trocken erscheinen. Zum Trost: Ihr könnt auch einfach die Zusammenfassung am Ende jedes Abschnitts lesen 😉 Sehr empfehlen möchte ich jedoch den letzten Fall „Schräges Ziehen“, da er von enormer praktischer Relevanz ist. Da ich stark vereinfache, ist er auch leicht verständlich. Doch genug der warmen Worte… Schauen wir uns jetzt die physikalischen Effekte beim Ziehen am Toilettenpapier genauer an!
Modell bei gleichmäßigem Ziehen
Ich habe zum besseren Verständnis eine kleine Skizze angefertigt. In der Abbildung unten seht ihr ganz links eine Rolle Toilettenpapier. Es bildet sich eine Abrollkante (A), dort wo die Blätterkette tangential die Rolle verlässt, und die Perforationen (Bi) dehnen sich gleichmäßig, wenn man am untersten Blatt (C3) über die gesamte Breite gleichmäßig zieht. Für unser Gedankenexperiment wollen uns vorstellen, dass die Rolle fixiert ist.
Die Toilettenpapierrolle lässt sich vereinfacht auch als Ersatzkonstruktion aus Federn darstellen; dies sehen wir in der Mitte der Abbildung. Jeder kennt das Hooksche Gesetz, nach dem der Zug an einer Feder elastisch ist – zumindest bis zum Erreichen der Streckgrenze. Wird die Streckgrenze erreicht, nimmt die Feder dauerhaft Schaden; will heißen, dass das Klopapier an der Perforation reißt 😉 Da die Blätter (Ci) deutlich weniger dehnbar sind als die Perforationen (Bi), kann die Wirkung der Blätter (bzw. harten Federn) vernachlässigt werden. Man erkennt das auch daran, dass sich beispielsweise die Ersatzfederkonstante dieser Reihenschaltung dadurch kaum ändert. Es ist somit legitim, auf das ganz einfache Modell rechts in der Abbildung zurückzugreifen, in dem nur noch die weichen Federn für die Perforation stehen.

Modelle bei gleichmäßigem Ziehen in Realität (links), als Ersatzschlatung (Mitte) und als vereinfachte Ersatzschaltung (rechts)
Und warum haben wir das jetzt gemacht? Ganz einfach: Man sieht deutlich, dass die Federn (bzw. Perforationen) sich bei Zug mit in einen gespannten Zustand begeben. Es wird klar, dass sich die Zugkraft nicht etwa der Länge nach über die Blätter und Perforationen verteilt: Egal wo man horizontal durch die Feder (bzw. entlang der Perforation) schneidet, wirken zwei Zugkräfte mit Betrag
und entgegengesetzter Richtung (Actio=Reactio). In der Abbildung oben habe ich dies an zwei Stellen symbolisch eingezeichnet.
Wie sich die Kraft über den Querschnitt verteilt, sollten wir noch etwas vertiefen… Die Perforation ist ja breit und es gibt mehrere Verbindungsfasern. Stellen wir uns vor, dass die Perforation in der Abbildung unten links nur aus drei Verbindungsfasern bestünde. Man könte dies statt mit einer Feder einfach mit drei parallelen Federn modellieren. Dabei wirkt in jeder Feder .

Modellierung der Spannung über den Querschnitt des Klopapiers in Realität (links) und im Modell (rechts)
Wenn man die Verteilung von Kraft in der Fläche beschreibt, nutzt man hierzu in aller Regel die Idee der mechanischen Spannung. Wir gehen von der Betrachtung einzelner Fasern der Perforation weg und betrachten die Perforation als kontinuierliche Strecke. Allgemein gilt . Wir wollen keine flächige sondern eine eindimensionale Kraftverteilung sehen (das Papier ist ja überall gleich dick; die Betrachtung der Dicke
ergäbe keinen Mehrwert). Daher schlage ich folgende Definition einer eindimensionalen Spannung vor:
Im weiter oben gezeigten Fall haben wir es mit einer konstanten Spannung zu tun. Hier ergäbe sich logischerweise
. Möchte man auch Fälle mit ungleichmäßiger Verteilung der Spannung behandeln, muss neben der Position entlang des Querschnitts
auch die Position entlang des Klopapierstranges
berücksichtigt werden. Deshalb erweitern wir die Definition auf
.
Bezüglich des Reißverhaltens von Toilettenpapier bei gleichmäßigem Ziehen, möchte ich konstatieren: Aus dem Modell ergibt sich erstmal kein Hinweis auf einen besonders strapazierten Bereich. Da in allen Perforationen die gleiche Spannung auftritt, ist vielmehr davon auszugehen, dass ein nicht ideal gleichmäßiges Ansetzen der Kraft oder eine unsaubere Verarbeitung an einer Stelle zum Reißen der Perforation führt.
Modell bei geradem Ziehen in einem Punkt
Wenn man an einem (idealisierten) Punkt des untersten Papier zieht, bewegt man diesen Punkt von der Abrollkante weg. Man erzeugt dabei eine Gegenkraft. Nun muss einem bewusst sein, dass sich diese Gegenkraft entlang der Klopapierlänge über Wirkungslinien als Spannung
verteilt, wobei
die Entfernung zum unteren Rand des untersten Blattes sein soll. Einige dieser Linien habe ich im Modell unten eingezeichnet – tatsächlich gibt es aber unendlich viele davon. Es gibt keine Wirkungslinien zu den Blatträndern jenseits der Abrollkante, da dort keine fixierten Punkte existieren.
Die größte Spannung ist und verläuft in Gegenrichtung zu
. Alle anderen Spannungen
weichen um den Winkel
von
ab. Gemäß Kräfteparallelogramm belaufen sie sich auf
. Schauen wir uns nun an, welcher Spannungsverlauf sich auf Höhe von
ergibt:
Der oben abgebildete Plot wurde für und
generiert. Die Spannung nimmt zu den Rändern hin ab; dies jedoch in enorm geringem Maße. Bei der Berechnung von
können wir daher leicht vereinfachen. Achtung: Das funktioniert nur in diesem konkreten Fall! In anderen Konstellationen muss ggf. der aufwändige Weg über eine Integration gegangen werden!
Unter und
verstehe ich die Grenzen der Wirkungslinien. Dieser Bereich wird von y=0 bis zur Abrollkante immer größer. Gemäß Strahlensatz müssen
und
proportional zu
sein. Daraus folgt:
Dies wiederum rechtfertigt die Ersatzschaltung.
Die untere Feder wird schneller an ihre Streckgrenze gelangen als die oberen parallel geschalteten Federn, auf die jeweils nur die halbe Kraft einwirkt. Ich habe es zwar nicht bewiesen, aber die folgende Erkenntnis gilt auch, wenn man jenseits der Blattmitte anfasst. Fazit: Zieht man am Klopapier gerade nach unten, so reißt das Toilettenpapier mit hoher Wahrscheinlichkeit nahe der Mitte der untersten Perforation!
Modell bei schrägem Ziehen
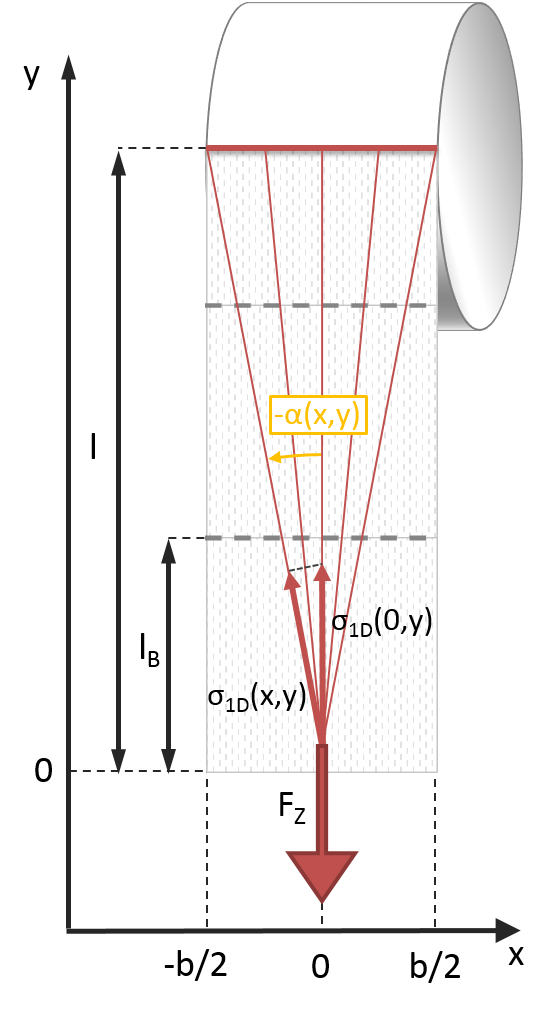
Unter „schrägem Ziehen“ subsummiere ich die Vorgänge, bei denen man nicht schön gerade nach unten sondern eben schief zieht. Überraschung! 🙂 Im Gegensatz zum vorangegangenen Abschnitt, beschränke ich mich nicht auf das Ziehen an einem Punkt. Da Finger breit sind, wollen wir diesmal annehmen, dass die Kraft in der gesamten Fläche, auf der die Finger aufliegen, angreift. Bei diesem Zugvorgang bildet sich statt einer Abrollkante ein Abrollpunkt, welchen ich in der Grafik unten auch eingetragen habe. An diesem Punkt bündelt sich die Spannung des Toilettenpapiers, da sich defacto alle Punkte des Toilettenpapiers von diesem einen Abrollpunkt entfernen während er dort fixiert ist. Charakteristisch ist auch die Papierwulst, welche sich direkt neben dem Abrollpunkt bildet.
Um die Frage zu beantworten, wo das Klopapier reißen wird, müssen wir uns Gedanken über den Spannungsverlauf machen. Dazu drehen wir unser Modell so, dass die Papierblätter wieder senkrecht nach unten zeigen. Da sich die Spannung im Toilettenpapier zum Abrollpunkt hin konzentriert, haben wir es mit dem entgegengesetzten Fall zum „geraden Ziehen in einem Punkt“ zu tun. Es gilt dann der unten dargestellte Spannungsverlauf.
Die Spannung in den Perforationen erhalten wir durch Analyse der Strecken b1 und b2. In der Abbildung oben ist offensichtlich, dass die mechanische Spannung zum linken Ende von b1 und b2 hin größer sein dürfte als auf der rechten Seite, da die linke Seite bereits näher am Abrollpunkt liegt als die rechte. Aufgrund der im allgemeinen Anwendungsfall auftretenden Winkel beim schrägen Ziehen, halte ich diesen Effekt aber für überschaubar (man denke nur an die Kopfstände für nichts und wieder nicht im vorhergehenden Abschnitt). In der weiteren Berechnung ignorieren wir ihn einfach. Unter der Annahme, dass die Spannung innerhalb jeder Perforation konstant ist, und des Strahlensatzes stoßen wir auf folgenden simplen Zusammenhang:
Das ist bemerkenswert, denn es beweist eindeutig, dass die Spannung in der obersten Perforation definitv am größten ist. Befindet sich die Perforation nur kurz unter Abrollkante, dann ist die Spannung in der obersten Perforation fast unendlich größer als in der folgenden Perforation! Gibt es viele Perforationen, läuft man aber in ein Quantisierungsproblem: Ab einer bestimmten Blattzahl sind die Abschnitte bi nahezu gleich groß; es gibt jedoch ein festes Raster von Fasern in der Perforation. Wenn in jeder der obersten Perforationen nur über einer einzigen Faser abfällt, besteht kein Unterschied zwischen den obersen Perforationen und eine Vorhersage wird unmöglich.
Fazit: Im gängigen Anwendungsfall wird die oberste Perforation reißen!
Zusammenfassung
Wir haben herausgefunden, dass
- Toilettenpapier mit hoher Wahrscheinlichkeit in der Mitte der untersten Perforation reißt, wenn man mittig am untersten Blatt zieht und
- Toilettenpapier mit hoher Wahrscheinlichkeit an der obersten Perforation reißt, wenn man schräg zieht.
Jetzt muss ich aber nochmal den Bogen zurück zur „Physik des Toilettenpapierspenders“ kriegen 😀 Wir haben formelmäßig gesehen, dass die Spannung extrem hoch werden kann, wenn man schräg zieht und sich eine Perforation in der Nähe des entstehenden Abrollpunktes befindet. Wenn man im Alltag an einem Toilettenpapierspender mit Abrollbremse am Toilettenpapier zieht, wird man in der Eile des Gefechts immer leicht schräg ziehen. Auch das Ziehen in einem Punkt führt zu einer erhöhten Spannung in der Perforation. Ist die benötigte Zugkraft (aus Gründen, die ich im Beitrag zum Toilettenpapierspender beschrieb) erhöht, kann dies das ungewollte Reißen des Klopapiers erklären.Heureka!














Schreibe einen Kommentar