Eine der Sachen, die ich nie so richtig nachvollziehen konnte, ist die Beziehung der Chi-Quadrat-Verteilung zur Stichprobenarianz. Diese Beziehung nutzt man beispielsweise, um bei vorliegender Stichprobenvarianz einer normalverteilten Grundgesamtheit auf die Varianz der Population zu schließen. Wir sprechen also über eines der wichtigeren Kapitel der Statistik. Lesen Sie weiter →
Was die Welt im Innersten zusammenhält
Ein wissenschaftlicher Blog über die verblüffenden Zusammenhänge der Welt
Schlagwort: Herleitung (page 1 of 2)
Zum Überschlagen von Erwartungswerten kann es hilfreich sein, wenn man Erwartungswerte multipliziert. Dieser Beitrag zeigt, dass es legitim ist Erwartungswerte zu multiplizieren, wenn es sich – anders als beim Addieren von Erwartungswerten – um Erwartungswerte unabhängiger Zufallsvariablen handelt. Da Mittelwerte Schätzer von Erwartungswerten sind, gelten die Ausführungen auch für Mittelwerte. Lesen Sie weiter →
Es handelt sich zwar um einen sehr intuitiven Aspekt der Statistik, der Vollständigkeit wegen sollte er aber nicht unerwähnt bleiben: Warum man Erwartungswerte addieren darf. Da Mittelwerte Schätzer von Erwartungswerten sind, gelten die Ausführungen auch für Mittelwerte. Lesen Sie weiter →
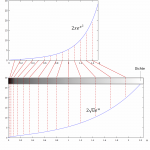
Im Alltag selten gebraucht und doch wichtig: Die Bogenlänge einer Funktion. Gemeint ist die Strecke, welche ein Graph innerhalb eines Intervalls bildet. Die Formel zur Berechnung für eine Funktion
lautet:
Und wie kommt man jetzt darauf? Lesen Sie weiter →
Dieser Beitrag wendet sich an alle, die hin und wieder Bluff spielen. Die Freunde der Mathematik finden wie immer eine ausführliche Herleitung der Ergebnisse. Interessiert sie euch nicht, dann überspringt ihr sie einfach 😉 Wer sich nicht an die Regeln erinnert oder noch nie in den Genuss dieses Spieles gekommen ist, sollte sich die Anleitung zu Bluff durchlesen.
Im Laufe des Spieles kommt man mehrfach zum Zug. Ihr müsst entscheiden, ob das Gebot des Vorgängers realistisch ist. Hat man bei Zügen eine Wahrscheinlichkeit
einen falschen Tipp abzugeben, dann ist die Anzahl der Fehlschläge binomial verteilt
. Die Wahrscheinlichkeit bei etwa 15 kritischen Zügen (mit scheinbar unrealistischen Geboten) weniger als 5 mal daneben zu liegen (und dadurch zu verlieren), ergibt sich zu Lesen Sie weiter →
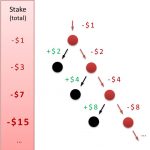
Damals, im Jahr 2010, betrat ich auf Teneriffa das erste mal ein Casino. Im Internet hatte ich einige Monate zuvor von der Strategie des „Verdoppelns“ oder „Doppelns“ beim Roulette gehört und wollte sie einmal ausprobieren. Man wählt dazu eine Farbe – Rot oder Schwarz – und setzt zunächst einen initialen (kleinen) Einsatz (z. B. 1€). Trifft die Kugel die gewählte Farbe, hätten wir schon unseren ersten Gewinn (1€) eingefahren. Verlieren wir, so setzen wir in der nächsten Runde den doppelten Betrag (2€) auf die gewählte Farbe. Sollten wir in dieser Runde gewinnen, erhalten wir das Doppelte des gesetzten Betrag (4€) und hätten nach Abzug der vorherigen Einsätze (in unserem Beispiel 3€) einen Euro Gewinn gemacht. Fällt in dieser Runde wieder ein Verlust an, dann verdoppeln wir den Einsatz immer weiter, bis wir gewonnen haben. Und obwohl ich damals zweimal innerhalb einer halben Stunde ca. 15€ Gewinn gemacht habe, stelle ich die Frage: Schlägt man beim Roulette so wirklich das Casino? Lesen Sie weiter →
Heute geht es wieder um die großen Geheimnisse des Universums. In „Physik des Toilettenpapierspenders“ habe ich versucht, dem Mysterium unvermitteltem Klopapier-Reißens auf die Schliche zu kommen. Es stellte sich jedoch heraus, dass es neben der Bauform des Toilettenpapierhalters noch weitere Faktoren geben muss, welche Risswahrscheinlichkeit und -position beeinflussen. Dieser Beitrag führt die begonnene Forschung fort und untersucht die Verteilung der Kraft beim Ziehen am Toilettenpapier – entweder an einem Toilettenpapierspender mit Abrollbremse und/oder bei ruckartigem Ziehen an einer Toilettenpapierrolle ohne Abrollbremse. Lesen Sie weiter →
Lange plagte mich die Frage, ob ich diesen Beitrag wirklich schreiben soll. Irgendwie hatte ich Angst, er könnte etwas lächerlich wirken. Inzwischen ist die Angst der Begeisterung über die Komplexität des Themas gewichen. Es geht um stille Geschäfte und moderne Technik 🙂 Lesen Sie weiter →
Ich lasse mich ja gern auf neue Standpunkte ein. Meinen Beitrag über die „Eine einfache Herleitung der Summe von Quadratzahlen“ halte ich nach wie vor für recht anschaulich. Allerdings ist der Ansatz dort nicht besonders generisch. Beispielweise können wir über die Summe kubischer Zahlen wie auch über die Summen höherer Ordnung keinerlei Aussage treffen. In einem Forenbeitrag habe ich von einem anderen Ansatz gelesen, welcher mich sehr beeindruckt hat. Daher möchte ich die Idee heute ausführlich darstellen. Lesen Sie weiter →
Früher hatten die Menschen wohl noch Zeit, um sich den wirklich interessanten Fragen des Alltags zu stellen. Thomas M. Cover stieß beispielsweise auf das Phänomen des Zwei-Zettel-Spieles. Die Idee ist simpel: Man nehme zwei Zettel und lasse von einer Person zwei zufällige (und sinnvollerweise auch unterschiedliche) Zahlen darauf schreiben. Nun darf man einen der beiden Zettel wählen. Nach Betrachtung der darauf notierten Zahl, muss man einen Tipp darüber abgeben, ob die Zahl auf dem anderen Zettel größer oder kleiner ist. Da es sich um beliebige Zahlen handeln kann, müsste die Wahrscheinlichkeit für einen korrekten Tipp bei 50% liegen. Tatsächlich gibt es aber eine Strategie, die mindestens 50% Trefferwahrscheinlichkeit erzielt. Es gibt Dinge, die sind schon verblüffend! Lesen Sie weiter →
© 2024 Was die Welt im Innersten zusammenhält
Theme by Anders Noren — Up ↑