Physik des Toilettenpapierspenders

Inhalt

Motivation
Das Modell
Interpretation
Ausblick

Lange plagte mich die Frage, ob ich diesen Beitrag wirklich schreiben soll. Irgendwie hatte ich Angst, er könnte etwas lächerlich wirken. Inzwischen ist die Angst der Begeisterung über die Komplexität des Themas gewichen. Es geht um stille Geschäfte und moderne Technik 🙂

Motivation

Professioneller Toilettenpapierspender

Bei der oben dargestellten Maschine handelt es sich nicht einfach nur um einen Toilettenpapierspender. Neben einer ausgefeilten Mechanik, um bei Bedarf auf die Reserverolle umschalten zu können, kommt diese Maschine mit einer „Abrollbremse“ daher. Eigentlich soll diese Bremse das unkontrollierte Abrollen des Toilettenpapiers unterbinden, wenn ihr mal wieder zu gierig an der Klopapierrolle gezogen habt. Offenbar führt dieses Bremssystem aber zu unkontrolliertem Papierabrissen, wenn sich nur noch wenige Blätter auf der Rolle befinden: Man zieht am ersten (sehr dünnen) Blatt, doch man braucht noch weitere Blätter. Plötzlich reißt das erste Blatt an der Perforation ab… Das ist ärgerlich, weil man dann anfängt, mit Toilettenpapierblättern zu hantieren. Aber warum ist das eigentlich so?

Das Modell

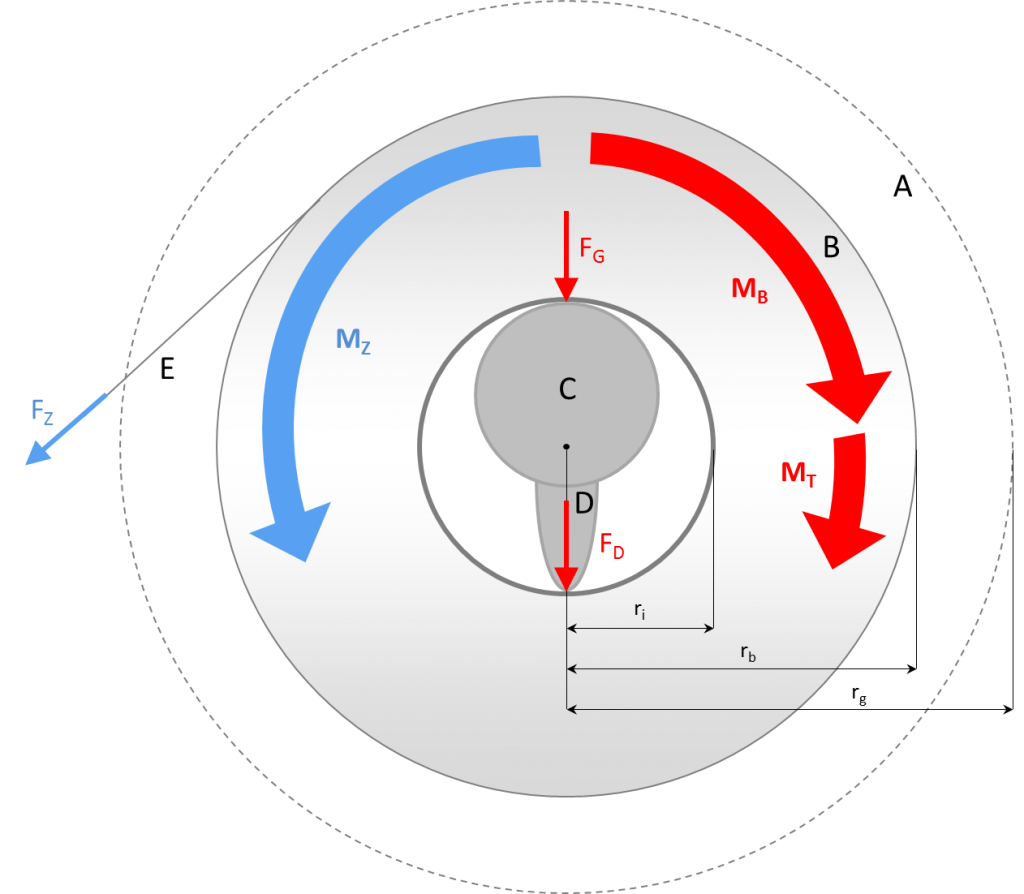
Zunächst betrachten wir den Querschnitt duch die Halterung. Wir sehen den maximalen Umfang der Toilettenpapierrolle (A) mit Radius $r_{g}\,$ , den aktuellen Umfang der Toilettenpapierrolle (B) mit Radius $r_{b}\,$ sowie das Blatt an dem aktuell mit der Kraft $F_{Z}\,$ gezogen wird (E). In der Mitte der Halterung befindet sich innerhalb der Toilettenpapierrolle mit Innenradius $r_{i}\,$ ein Plastikzylinder (C), aus dessen Unterseite eine Art federgespannter Hebel (D) herausgedrückt wird. Durch die Gewichtskraft der Toilettenpapierrolle auf den Zylinder $F_{G}\,$ und die Federkraft $F_{D}\,$ wird die Bremsung erzeugt.

Physikalisches Modell der Toilettenpapier-Halterung und teilweise verbrauchter Papierrolle

Physikalisches Modell des Toilettenpapierspenders und teilweise verbrauchter Papierrolle

Ausgangspunkt des Modells ist die Drehmomentenbilanz, wobei das durch die Zugkraft generierte Moment $M_{Z}\,$ mindestens das Bremsmoment $M_{B}\,$ betragen muss. Bleibt noch etwas über, überwindet dieses verbleibende Moment $M_{T}\,$ die Trägheit und versetzt die Toilettenpapierrolle somit in Bewegung.

$\displaystyle M_{Z}=M_{B}+M_{T}$

Recht schnell können wir die Kräfte über entsprechende Hebelarme ins Spiel bringen:

$\displaystyle F_{Z} \cdot r_{b}=r_{i} \cdot \mu \cdot (F_{G}+F_{D}) + J \cdot \alpha$

Die Gewichtskraft $F_{G}\,$ hängt vom initialen Gewicht $m_{v}\,$ und vom Blattbestand in Form von $r_{b}\,$ ab. Auch das Trägheitsmoment $J\,$ der Klopapierrolle hängt vom aktuellen Radius $r_{b}\,$ und dem aktuellen Gewicht der Rolle ab. Dieses Gewicht hängt selbst von $r_{b}\,$ ab. Da man beim Ziehen an der Rolle immer „auf der Geraden“ beschleunigt, muss auch bei der Bestimmung der Winkelbeschleunigung $\alpha$ eine Umrechnung stattfinden. Die hängt natürlich auch von $r_{b}$ ab 😉

$\displaystyle F_{Z} \cdot r_{b}=r_{i} \cdot \mu \cdot \Big(m_{v}\cdot g \cdot \frac{r_{b}^{2}-r_{i}^{2}}{r_{g}^{2}-r_{i}^{2}}+F_{D}\Big) + m_{v} \cdot \frac{r_{b}^{2}-r_{i}^{2}}{r_{g}^{2}-r_{i}^{2}} \cdot \frac{r_{b}^{2}+r_{i}^{2}}{2} \cdot \frac{a}{r_{b}}$

Es existieren zwar viele unbekannte Größen, die wir auch noch schätzen werden, letztlich halte ich aber die Definition der Zugkraft $F_{Z}\,$ als Funktion des gegenwärtigen Rollenradius $r_{b}\,$ und der Beschleunigung beim Ziehen am ersten Blatt $a\,$ für sinnvoll. Diese Größen ändern sich nämlich auch bei vollkommen bekanntem Setup.

$\displaystyle F_{Z}\big(r_{b}, a \big) :=\frac{r_{i}}{r_{b}} \cdot \mu \cdot \Big(m_{v}\cdot g \cdot \frac{r_{b}^{2}-r_{i}^{2}}{r_{g}^{2}-r_{i}^{2}}+F_{D}\Big) + m_{v} \cdot a \cdot \frac{r_{b}^{4}-r_{i}^{4}}{2 \cdot r_{b}^{2} \cdot (r_{g}^{2}-r_{i}^{2})}$

Interpretation

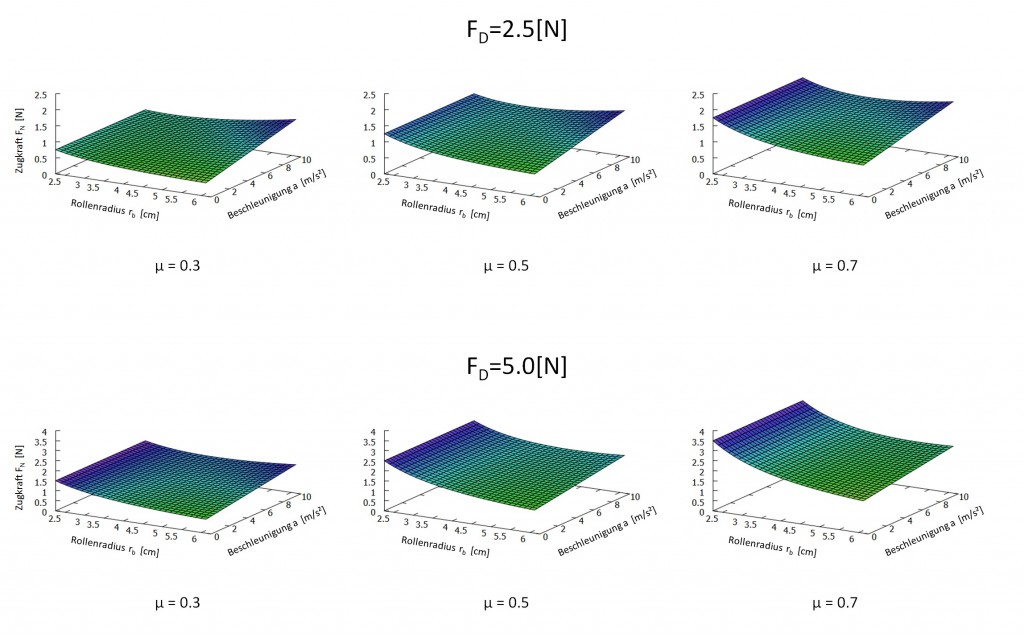
Nun habe ich einfach mal zum Lineal gegriffen und für eine 3-lagige Klopapierrolle mit 180 Blatt $r_{i}=0.0225\, cm\,$ , $r_{g}=0.0625\, cm\,$ und $m_{v}=0.135\, kg\,$ ermittelt. Außerdem habe ich während einer dienstlichen Sitzung mal die Zeit genutzt und am Hebel des CWS-Spenders herumgedrückt. Beim Vergleich mit Gewichten, würde ich $F_{D}\,$ zwischen 2,5N und 5N einordnen. Für die Materialien Pappe und Kunststoff konnte ich online keine passenden Reibungspaarungen finden. Alternativ habe ich mir die Werte für Pappe auf verschiedenen Materialien angesehen und auch die Werte von Kunststoff auf verschiedenen Materialien. Ich halte einen Haftreibungskoeffizienten zwischen 0,5 und 0,6 ebenso realistisch wie einen Gleitreibungskoeffizienten von 0,3. Die entsprechenden Plots seht ihr unten (ACHTUNG: Die Skalierung der Zugkräfte unterscheidet sich zwischen beiden Zeilen!) .

Plots des Modells für verschiedenen Reibungskoeffizienten und Federkräfte

Was wir herauslesen können: Je höher die Federkraft der Abrollbremse gewählt wird, umso größer ist der Anstieg der benötigten Zugkraft bei sich leerender Toilettenpapierrolle. Die Beschleunigung beim Ziehen zeigt in allen Plots nur bei relativ gefüllter Toilettenpapierrolle einen Einfluss auf die benötigte Zugkraft – ist die Rolle leer, ist der Einfluss nahe Null (da dann nur noch die Pappe dranhängt).

Was sich schlussfolgern lässt: Die Plots zeigen eindeutig, dass man mehr Zugkraft aufbringen muss, wenn sich die Toilettenpapierrolle ihrem Ende nähert. Sobald die Zugkraft größer wird als die maximal verträgliche Spannungskraft im Klopapier, reißt es. Wir können also folgern, dass ein unerwünschtes Reißen wahrscheinlicher wird. Genauer können wir es nicht sagen, da diese maximale Spannungskraft im Toilettenpapier stark von der Anzahl der Lagen, der Papierbeschaffenheit und auch von der Art der Perforation abhängt (ja: Klopapier ist ein High-Tech-Produkt!).

Ausblick

In diesem Beitrag habe ich einige Mechanismen untersucht, die zu einem frühzeitigen Reißen des Toilettenpapiers führen können. Vor allem der Toilettenpapierspender stand als Corpus Delicti im Mittelpunkt. Der Hersteller kann hier in Zukunft durchaus noch Potenziale ausschöpfen, wenngleich die Abrollbremse bereits heute eine große Hilfe ist.

Allerdings fallen mit noch viele weitere Einflussfaktoren ein. Beispielsweise sind die Radien des Klopapiers häufig lageabhängig, weil die Rollen nicht ideal kreisrund sondern „geknüllt“ sind. Anhand der Abbildung unten, kann man sich vorstellen, dass die benötigte Zugkraft durch diesen Effekt sehr stark schwankt. Alle physikalischen Effekte exakt zu untersuchen, wäre aber vermutlich Rocket-Science…

Unterschied der idealen zur realen Toilettenpapierrolle

Einem anderen Thema würde ich indes sehr gern in einem weiteren Beitrag nachgehen: Die Physik des Toilettenpapiers! Wirkt eigentlich überall im Toilettenpapier die gleiche Kraft? Und warum reißt das Toilettenpapier dann eigentlich fast immer an dem Blatt, welches sich am nächsten an der Rolle befindet? Und obwohl wir gesehen haben, dass die Beschleunigung beim Ziehen an einer fast leeren Rolle kaum Einfluss hat: Macht es doch irgendwie einen Unterschied, ob man vorsichtig oder weniger vorsichtig am Toilettenpapier zieht? Es bleibt also spannend!

Nachtrag: Im Beitrag „Physik des Klopapiers“ habe ich nachträglich herausgefunden, dass das Toilettenpapier reißt, weil man das Papier in der Regel schräg zur Seite zieht. Dadurch konzentriert sich die Zugkraft in der obersten Perforation und führt mit hoher Wahrscheinlichkeit zum Reißen. Die Wahrscheinlichkeit steigt mit größerer Zugkraft; die Gründe hierfür habe ich oben dargestellt.