Wer schon einmal mit diskreten Zufallsvariablen zu tun hatte, der weiß, dass man den Erwartungswert manchmal vor lauter Summenzeichen nicht mehr erkennt 🙂 In der Regel kommt man in der Welt der kontinuierlichen Statistik deutlich schneller ans Ziel. Daher zeige ich heute, wie man den Erwartungswert einer diskreten Zufallsvariable über die analoge kontinuierliche Verteilung nähern kann.
Diskret
Der Erwartungswert diskreter Zufallsvariablen berechnet sich als Summe aller möglichen Werte, multipliziert mit deren Wahrscheinlichkeit. Die Werte ergeben sich aus dem Sachverhalt und die Wahrscheinlichkeiten – nun ja – eben aus der Wahrscheinlichkeitsverteilung 😉
Nehmen wir dazu ein altbekanntes Beispiel her: Würfeln. Für einen sechsseitigen ungezinkten Würfel kommen wir auf den Wert, welchen wir ja aus der Schule bereits kennen:
Was wir hier getan haben ist ja eher so etwas wie „numerisches Bestimmen“ des Erwartungswertes. Um eine allgemeine Formel für einen n-seitigen Würfel angeben zu können, bedarf es der Gaußschen Summenformel. Damit ergibt sich die nachfolgende Formel.
So einfach wie im Fall der Gaußschen Summenformel lassen sich die Summenterme aber selten ersetzen. Um nicht in die Untiefen von Reihen und Folgen abtauchen zu müssen, werden wir versuchen, die Formel auch ohne Herrn Gauß herzuleiten!
Kontinuierlich
Tauschen wir also Summe gegen Integral, Wahrscheinlichkeitsverteilung gegen Dichtefunktion und die diskrete Laufvariable gegen ein kontinuierliches
:
Zuerst sollten wir kurz den Übergang der diskreten Wahrscheinlichkeitsverteilung in die Dichtefunktion f(x) betrachten. Statt mit diskreten Werten muss diese mit Intervallen befüttert und integriert werden, da sie per Definition an einer einzelnen Stelle 0 ist.
Wie man sieht, kommt man durch Integration der uniformen Dichtefunktion mit Betrag 1/n letztlich auch zur Wahrscheinlichkeit von 1/n für die einzelnen Würfelergebnisse . Der ein oder andere mag sich jetzt wegen der Integrationsgrenzen irritiert zeigen. Prinzipiell hätte ja auch die Integration von
bis
das gleiche Ergebnis zu Tage gefördert. Spätestens bei der Berechnung des Erwartungswertes löst die Wahl dieser Intervallgrenzen aber einige Probleme, da
um den Wert von
herum im Mittel zu
wird. Dies ist für die Approximation von sehr großer Bedeutung. Nun aber zurück zur Berechnung des Erwartungswertes:
Was für eine Überraschung: Wir kommen auf den gleichen Term wie der, den wir eingangs als exakte Formel für den Erwartungswert der gleichverteilten Zufallsvariable X kennengelernt haben! Fairerweise muss man jedoch auch erwähnen, dass dies nur in diesem Fall so hervoragend funktioniert, weil die Dichtefunktion konstant ist und dadurch wie ein Faktor um das Integral wirkt, welches sich bei den gewählten Integrationsgrenzen wiederrum wie
verhält.
Etwas weniger Linearität bitte!
Was in diesem einfach Beispiel funktioniert hat, geht natürlich auch komplizierter 🙂 Wir können den Erwartungswert beliebiger Transformationen von X nähern:
Als Beispiel können wir ja mal schauen, welchen Erwartungswert wir erhalten, wenn wir die Zahlen des n-seitigen Würfels quadrieren. Dabei ist wodurch sich nach Einsetzen folgendes Resultat einstellt.
Nur mal zum Vergleich: Für einen 6-seitigen Würfel ist der Erwartungswert tatsächlich während die Approximation 15,25 ergibt. Es existieren weniger lineare Näherungen also durchaus Abweichungen. Diese Abweichungen, also den Fehler der Approximation, werde ich in meinem nächsten Beitrag genauer untersuchen. Es bleibt also spannend!
Nachtrag:
Zum Thema Abweichung der Approximation habe ich den Artikel „Fehlerbetrachtung bei der Approximation diskreter Erwartungswerte“ online gestellt.

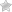 (2 Stimmen, Durchnschnitt: 4,00 von 5)
(2 Stimmen, Durchnschnitt: 4,00 von 5)




Schreibe einen Kommentar