In meinen früheren Beiträgen habe ich bereits über Addieren und Multiplizieren von Mittel- und Erwartungswerten berichtet. Was das Dividieren angeht, möchte ich jedoch etwas zur Vorsicht mahnen. Man muss genau schauen, ob tatsächlich der Kehrwert vom Mittelwert gemeint ist!
Man bedenke folgendes Beispiel: Alex behält seine Autos in der Regel für ein Jahr, Ina zwei Jahre und Peter 9 Jahre. Im Mittel behalten sie die Autos also 4 Jahre. Heißt das nun, dass die drei Personen im Durchschnitt 10/4=2,5 Autos pro 10 Jahre besitzen? Sehen wir uns die Sache anhand des Bildes unten genauer an.
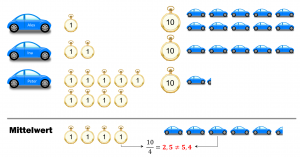
Das Reziproke des Mittelwertes der Besitzdauer entspricht nicht dem Mittelwert der Autos je 10 Jahre
Lesen Sie weiter →