Vor Kurzem fragte ich mich, wie man wohl die Verteilungsfunktionen des Produktes zweier unabhängiger Zufallsvariablen bestimmen könne. Nachdem die Internetrecherchen nicht viel hergaben, musste ich meinen Hirnschmalz zusammennehmen… und meine Erkenntnisse mit euch teilen 🙂
Allgemeiner Fall
An sich ist die Berechnung ganz einfach. Man möge einfach die entstehende Zufallsvariable betrachten. Die möglichen Paarungen der Faktoren
und
lassen sich als Graph darstellen, da
. Ich habe die Darstellung hier – der Einfachheit wegen – auf
und
beschränkt.
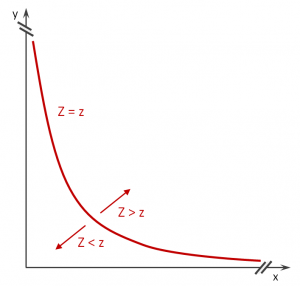
Für alle denkbaren Werte von Z ergibt sich eine Kurvenschar, welche die Paarung möglicher Faktoren beschreibt.
Man müsste nun nur die Wahrscheinlichkeiten entlang des Graphen integrieren, um
zu erhalten. Dies ist leider nicht so ohne Weiteres möglich. Was also tun?
Wir können problemlos die kumulative Wahrscheinlichlichkeitsfunktion bestimmen, wenn für jedes über die Wahrscheinlichkeiten zu allen Punkten unterhalb der zu
passenden Hyperbel integrieren. Wenn man sich die Grafik oben als Draufsicht auf ein Gebirge vorstellt, dann entspräche dies dem Volumen des gedachten Gebirges. Konkret bedeutet das:
Da und
unabhängig und Wahrscheinlichkeiten immer positiv sind, kann vereinfacht werden zu:
Aus der kumulativen Wahrscheinlichkeitsfunktion wiederrum, können wir die Wahrscheinlichkeitsdichtefunktion ermitteln. Diese lässt sich definitionsgemäß durch Ableiten bestimmen.
Beispiel anhand gleichverteilter Zufallsvariablen
Schauen wir uns ein Beispiel an, bei dem und
zwischen 0 und 10 gleichverteilt sind. Es gilt also
bzw.
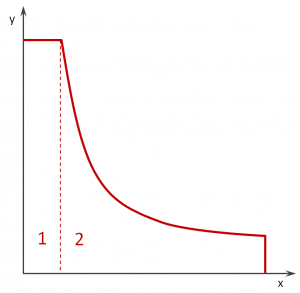
. Da die Verteilung der Zufallsvariablen nicht stetig ist (unter 0 und über 10 ist die Wahrscheinlichkeit 0), können wir nicht einfach in die Formeln von oben einsetzen. Stattdessen müssen wir etwas um die Ecke denken und das Integral in geeignete Stücke zerlegen (weshalb ich dieses Beispiel gewählt habe… ^^).
Um die kumulative Wahrscheinlichkeitsfunktion zu berechnen, werden wir einfach annehmen, dass die Wahrscheinlichkeit für alle passenden Paarungen jeweils 1/100 sein wird. Wie die oben gezeigte Skizze illustriert, ist die Hyperbel wegen der Beschränkung der Werte gestutzt. In unserem Fall geschieht dies sobald eine der Zufallsvariablen größer als 10 wird. Wenn wir uns an den Grundgedanken aus dem vorangehenden Abschnitt erinnern, müssen wir nur über die Wahrscheinlichkeiten unterhalb des gezeigten Graphen integrieren. Dazu teilen wir die Funktion in zwei Teile. Das tun wir dort, wo die Grenze von verletzt wird:
Wir berechnen alle Werte mit durch Wahl der festen Obergrenze „10“. Im verbleibenden Bereich gehen wir wie gehabt vor.
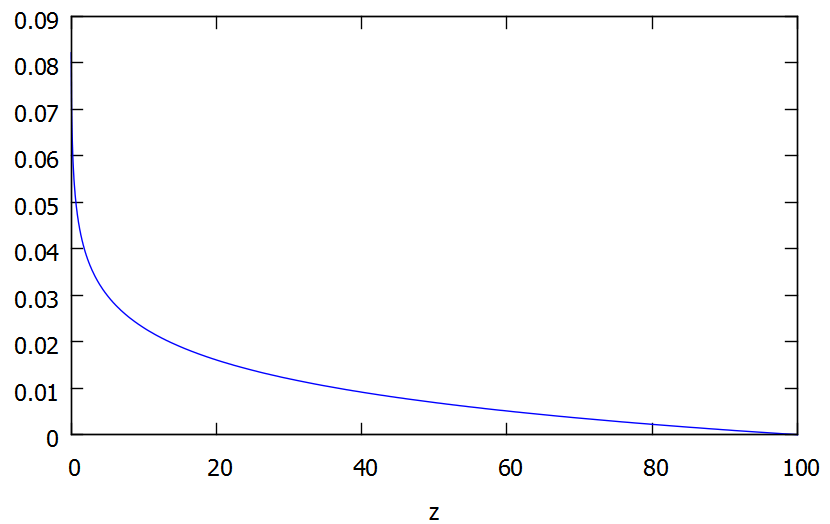
Nun differenzieren wir noch schnell nach – eine Tätigkeit, die ich bis auf einige Optimierungen dem CAS Maxima überlassen habe.
Und so sieht unsere Wahrscheinlichkeitsdichtefunktion aus:
Ausblick
Wie wir gesehen haben, kann die Berechnung einer konkreten Verteilung zweier Zufallsvariablen einen gewissen Aufwand fordern. Mit etwas Geschick können wir so aber verschiedene praktische Aufgaben lösen. Zum Beispiel könnte ja die Verteilung der Besucher eines Parkplatzes sowie die Verteilung der PKW-Breite bekannt sein. Dann is est möglich, eine Aussage über den benötigten Platz auf dem Parkplatz zu treffen. Prinzpiell können wir auch mehr als zwei Variablen miteinander verknüpfen, denn schließlich gilt ja 😉 Bei sehr vielen multiplikativ verknüpften Variablen ist es jedoch ratsam auf die Log-Normal-Verteilung zurückzugreifen, da man sich damit viel Arbeit sparen kann. Sicher werde ich diese spezielle Verteilung in einem der nächsten Beiträge vorstellen 🙂

 (3 Stimmen, Durchnschnitt: 4,00 von 5)
(3 Stimmen, Durchnschnitt: 4,00 von 5)



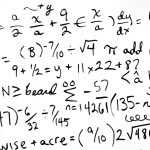

Schreibe einen Kommentar