In ihrem Beitrag „Warum es keine 140jährigen Menschen gibt“ beschreibt die sympathische Autorin, weshalb die Wahrscheinlichkeit sehr gering ist, dass ein Mensch in die Alterssphären von 110, 120 oder gar 130 Jahren vordringt. Demnach erreichen beispielsweise von tausend 100jährigen gerade einmal 6 ein Alter von 110. Die Rechnung ist durchdacht und hinsichtlich ihrer Schlüsse kann ich der Autorin in weiten Teilen reinen Gewissens folgen. Nichtsdestotrotz erscheinen einige Zwischenergebnisse unter Berücksichtigung von Wahrscheinlichkeitsverteilungen in einem ganz anderen Licht – wie ich zeigen werde!
Die Berechnungen beruhen auf der Sterbetafel der Statistik Austria. Von 2474 Menschen im Alter von 99 Jahren starben (ohne Rücksicht aufs Geschlecht) im Jahr 2014 944. Die Sterbewahrscheinlichkeit ergibt sich im Wesentlichen zu . Wen es wundert, dass in der Sterbetafel 0,38145 steht: Die bundesdeutschen Kollegen Eisenmenger und Emmerling zeigen, dass es aufgrund von „Wanderungen“ (z. B. Umziehen ohne Abmeldung am alten Wohnort) zu einer signifikanten Anzahl von Karteileichen kommt. Es findet folglich noch eine leichte Korrektur statt. Jetzt ist es aber so, dass die Sterbewahrscheinlichkeit nur ein Schätzwert dieser konkreten Stichprobe ist. Sei
die Anzahl sterbender Menschen im Alter von 99 Jahren. Die Zufallsvariable ergibt sich aus einer Kette von Bernoulli-Experimenten. Das Ergebnis ist eine Binomialverteilung, die aber auch durch eine Normalverteilung angenähert werden kann:
Dividiert man nun durch , erhält man die Zufallverteilung des Schätzers für die Wahrscheinlichkeit
Wir können auf Basis dieser Verteilung ein 90%-Konfidenzintervall von (0,36541; 0,39793) bzw. – auf die Angaben aus der Sterbetafel bezogen – etwa (0,36530; 0,39782) angeben. Errichtet man dieses Intervall, ist in 90% der Fälle die tatsächliche Wahrscheinlichkeit im Intervall enthalten. Plausible Werte für die echte Wahrscheinlichkeit sind (basierend auf unserer Stichprobe) somit Werte zwischen 0,36530 und 0,39793.
Die Autorin des benannten Beitrages nimmt nun an, dass die Sterbewahrscheinlichkeit auch über das Alter von 100 Jahren hinaus auf diesem Niveau bleibt. Korrekterweise gibt sie an, hier einen sehr optimistischen Fall zu betrachten. Genau genommen können wir das aber gar nicht einschätzen, denn wir haben ja keine Daten 😛
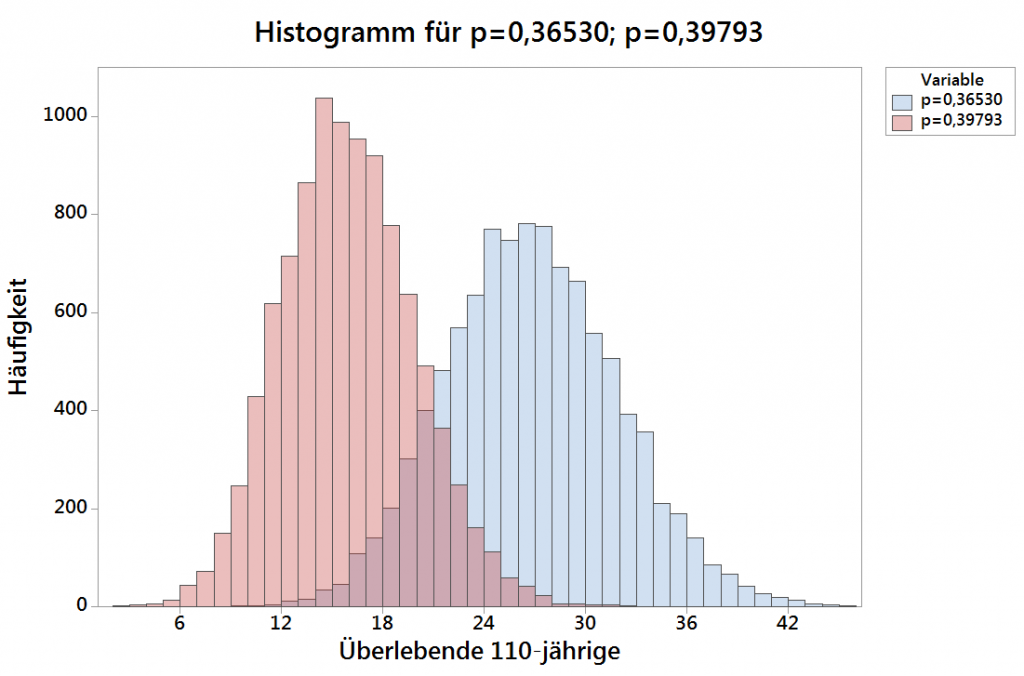
Um einen ersten Eindruck von der Verteilung überlebender 110-jähriger zu erhalten, habe ich eine kleine Simulation geschrieben und mit Hilfe von Minitab einen schönen Plot erzeugt. Die beiden Histogramme für 10000 Durchgänge mit einer Startpopulation von 2474 Menschen und den beiden Sterbewahrscheinlichkeiten 0,36530 und 0,39793 seht ihr unten.
Wir können daraus bereits eine Menge mehr Informationen gewinnen als nur zu sagen: Der Erwartungswert liegt bei rund 15 bzw. 26. Die Anzahl überlebender 110-jähriger streut stark; gemessen an den 25%- und 75%-Quantilen erscheinen 13 bis 30 überlebende 110-jährige relativ plausibel! Interessant ist auch, dass die Zufallsvariable ähnlich einer Normalverteilung aufgebaut ist.
Tatsächlich handelt es sich um eine Binomialverteilung, bei der sich die Wahrscheinlichkeit für das Überleben nach einer bestimmten Anzahl von Jahren aus der kumulierten Wahrscheinlichkeitsfunktion einer geometrischen Verteilung ergibt. Die Wahrscheinlichkeit für das Überleben von mindestens Personen in Abhängigkeit der Anzahl der Jahre
, der Sterbewahrscheinlichkeit
und der Startpopulation
kann berechnet werden wie folgt.
In diesem Modell finden wir auch den von der Autorin postulierten Erwartungswert von 6 110-jährigen wieder, wenn man 1000 100-jährige mit einer jährlichen Sterbewahrscheinlichkeit von 40% allein lässt:
Statt den Erwartungswert der exakt 110-, 120- und 130-jährigen zu betrachten, schlage ich vor einmal anzunehmen, wir hätten jedes Jahr 1000 100-Jährige, die wir beobachten. Wie hoch ist dann im stationären Zustand der Erwartungswert aller Menschen, die älter als 110 Jahre alt sind?
Natürlich basieren alle Berechnungen auf geschätzten Sterbewahrscheinlichkeiten. Insofern ist der ganze Beitrag ohnehin nur Kaffeesatzleserei 😀 Abgesehen davon, auf der mathematischen Spielwiese etwas vorzuturnen, hatte ich ein anderes Ziel. Mir ging es darum, die Gefahren von einzelnen isolierten Kennzahlen aufzuzeigen. Statistik ist eine sehr genaue Sache. Die Genauigkeit bemisst sich jedoch nicht an der Anzahl der Stellen hinter dem Komma, sondern an der Qualität der Statistik. Selbst wenn wir eine offizielle Sterbetafel vor uns haben, dürfen wir die Sterbewahrscheinlichkeit nicht als gesetzt betrachten. Auch beim Herausarbeiten eigener Analysen, sollte man eine möglichst umfassende Darstellung, welche über Erwartungswerte hinausgeht, wählen.
Mein Dank gilt an dieser Stelle iscribo für die schöne Vorlage.

 (2 Stimmen, Durchnschnitt: 4,50 von 5)
(2 Stimmen, Durchnschnitt: 4,50 von 5)




30. Dezember 2015 at 7:36
Mit dieser fundierten Analyse kann mein armseliger Beitrag natürlich nicht mithalten, das ist sozusagen Wahrscheinlichkeitsrechnung für das gemeine Volk. Statistik war ehrlich gesagt beim Studium nicht meine Stärke, heute wäre das möglicherweise anders
30. Dezember 2015 at 16:19
Wir haben eben unterschiedliche Zielgruppen 😉