Dieser Beitrag wendet sich an alle, die hin und wieder Bluff spielen. Die Freunde der Mathematik finden wie immer eine ausführliche Herleitung der Ergebnisse. Interessiert sie euch nicht, dann überspringt ihr sie einfach 😉 Wer sich nicht an die Regeln erinnert oder noch nie in den Genuss dieses Spieles gekommen ist, sollte sich die Anleitung zu Bluff durchlesen.
Im Laufe des Spieles kommt man mehrfach zum Zug. Ihr müsst entscheiden, ob das Gebot des Vorgängers realistisch ist. Hat man bei Zügen eine Wahrscheinlichkeit
einen falschen Tipp abzugeben, dann ist die Anzahl der Fehlschläge binomial verteilt
. Die Wahrscheinlichkeit bei etwa 15 kritischen Zügen (mit scheinbar unrealistischen Geboten) weniger als 5 mal daneben zu liegen (und dadurch zu verlieren), ergibt sich zu:
In 19 von 20 Spielen würden wir also gewinnen. Nun nutzen wir die ermittelte Wahrscheinlichkeit und setzen sie in eine fundierte Entscheidungsgrundlage um. Die Wahrscheinlichkeit für mehr als
Würfel mit gleicher Augenzahl (inklusive Sterne als Joker) bei insgesamt
Würfeln berechnet sich zu
Die Wahrscheinlichkeit für mehr als Würfel mit Sternen bei insgesamt
Würfeln berechnet sich zu
Die Wahrscheinlichkeit, bei einem Tipp daneben zu liegen, sollte im Mittel nicht größer als sein. Da die Formeln aber relativ unhandlich sind, habe ich die Wahrscheinlichkeiten in einem Excel-Sheet zusammengefasst. Bietet der Vorgänger also
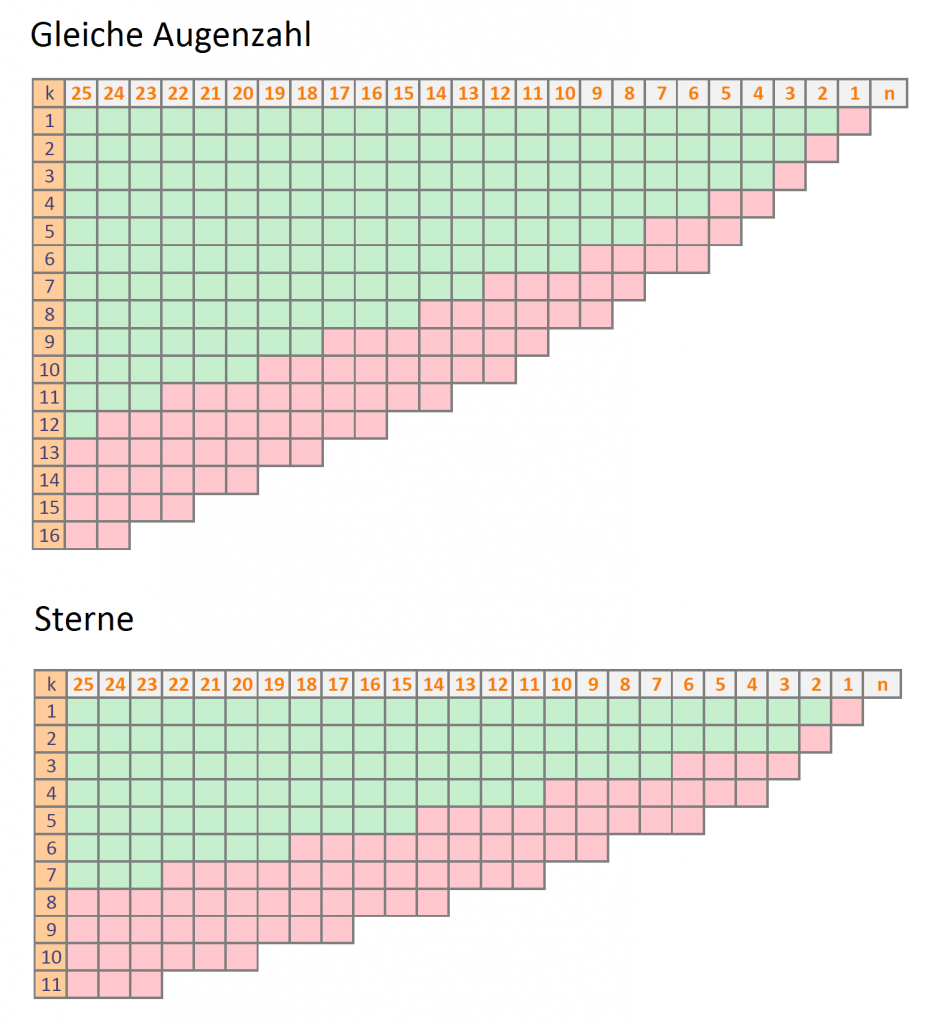
gleiche Augenzahlen, dann schaut ihr in der k-ten Zeile und der n-ten Spalte (für die Gesamtzahl der Würfel im Spiel). Ist diese Zelle rot markiert, dann ist die Aussage eures Vorgängers anzuzweifeln. Ihr könnt euch als Hilfe auch die folgende Grafik zum Spiel mitnehmen:
Wichtig: Die maximale Wirkung entfaltet dieser Ansatz, wenn man auch die Informationen der eigenen Würfel mit einbezieht. Euer Vorgänger gibt beispielsweise an, dass bei insgesamt 15 Würfeln 9 mal die „5“ im Spiel sei. Gemäß unserer Formeln ergibt sich die Wahrscheinlichkeit hierfür zu 0,031, was nicht akzeptabel ist. Jetzt habt ihr aber selbst noch 4 Würfel und darunter zweimal die „5“. Man muss nun nach der Wahrscheinlichkeit für 9-2=7 mal die „5“ bei 15-4=11 Würfeln im Spiel schauen. Die Wahrscheinlichkeit liegt bei 0,122 – also dem Dreifachen.Das Gebot ist somit realistisch und muss doch nicht unbedingt abgelehnt werden.
Man kann sich natürlich darüber streiten, ob es sich hier im engeren Sinne um eine Strategie für Bluff handelt. Der Ansatz zielt darauf ab, durch disziplinerte und rationale Anwendung der Wahrscheinlichkeitsrechnung Vorteile zu erzielen. Wenn auch seltener, seht ihr euch aber weiterhin einem Dilemma gegenüber: Das Gebot des Vorgängers ist nah an der Grenze zur Unwahrscheinlichkeit und (euer noch unrealistischeres) Gebot wird im nächsten Zug abgelehnt. Auch gegen Ende des Spiels helfen die Wahrscheinlichkeiten nicht weiter, da man fast immer ablehnen müsste. Wen dieses Problem interessiert, der kann unter diesem Link weiterlesen.
Ich wünsches fröhliches Bluffen!


 (17 Stimmen, Durchnschnitt: 3,29 von 5)
(17 Stimmen, Durchnschnitt: 3,29 von 5)





Schreibe einen Kommentar