Warum Integration durch Substitution wirklich funktioniert!

Integration durch Substitution ist eine mächtige Technik, die jedoch leider nicht ganz intutiv zu verstehen ist. Für mich war es während des Abiturs ein wahre Qual… Dieser Beitrag zielt darauf ab, das Vorgehen so zu illustrieren, dass es einem Substitutions-Novizen verständlich wird.

Was man mit Integration durch Substitution erreichen kann

Mal angenommen, man möchte sich an folgendes Integral heranwagen:

$\displaystyle \int x \sqrt{x-1}\, dx$

Ihr könnt nicht einfach drauf los integrieren, weil ein Ausdruck unter der Wurzel steht. Substituiert man aber $u=x-1$ , ergibt sich ein Standard-Integral. Also $x=u+1$ eingesetzt und:

$\displaystyle \int (u+1) \times \sqrt{(u+1)-1}\, dx=\int (u+1) \times \sqrt{u}\, dx=\int \sqrt{u^{3}}+\sqrt{u}\, dx$

Das ist narütlich deutlich einfach. Wir erhalten:

$\displaystyle \int \sqrt{u^{3}}+\sqrt{u}\, du=\frac{2u^{\frac{5}{2}}}{5}+\frac{2u^{\frac{3}{2}}}{3}+c$

Durch Rücksubstitution von $u=x-1$ erhalten wir die Lösung in Bezug auf $x$ :

$\displaystyle \int x \times \sqrt{x-1}\, dx=\frac{2(x-1)^{\frac{5}{2}}}{5}+\frac{2(x-1)^{\frac{3}{2}}}{3}+c$

Doch was ist eigentlich durch die Substitution passiert? Das nachfolgende Bild zeigt, dass durch die Substitution eine horizontale Verschiebung der Funktion stattfindet.

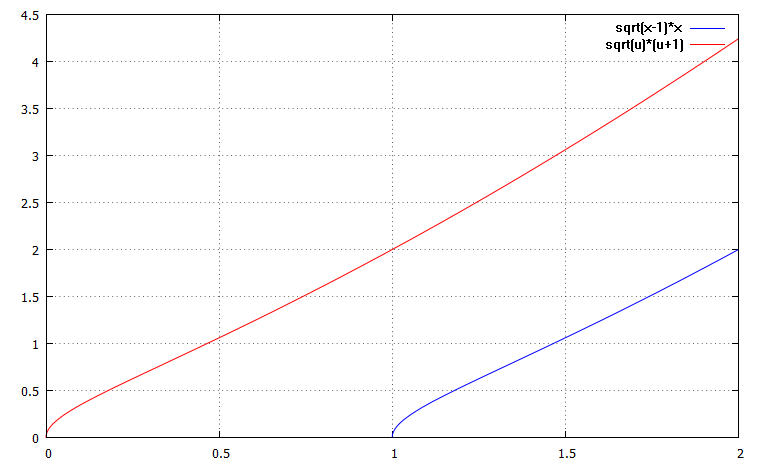
Eine lineare Substitution verschiebt die Funktion hat aber keine Auswirkung auf die Fläche unter dem Graphen

Allerdings findet in diesem Fall auch keine Änderung der Fläche unter dem Graphen statt. Deshalb funktioniert die Substitution hier. In den meisten Fällen ist dies aber anders und es muss noch ein wichtiger und oft unterschätzter Schritt gegangen werden! (siehe nächster Abschnitt)

Auch dx will substituiert werden!

Bis jetzt haben wir auf die Substitution von $dx$ verzichtet. Stattdessen wurde $dx$ schlicht durch $du$ ersetzt, was aber eigentlich nicht zulässig ist und nur für lineare Verschiebung funktioniert. Lasst uns daher versuchen, $2xe^{x^2}$ zu integrieren. Gemäß umgekehrter Kettenregel der Differentialrechnung, ergibt sich völlig klar

$\displaystyle \int 2xe^{x^2}\, dx=e^{x^2}+c$

Die Substitution $u=x^2$ (also $x=\sqrt{u}$ ) ergibt aber

$\displaystyle \int 2\sqrt{u}e^{u}\, du$

was nun leider nicht dem vorher genannten korrekten Ergebnis entspricht. Wo liegt das Problem? Ganz einfach! Die Substitution hat die Form der Funktion verändert. Die folgende Abbildung zeigt die Zuordnung gleicher Funktionswerte unserer Funktion vor (oben) und nach (unten) Substitution. Man erkennt klar, dass die Funktion nach Substitution (unten) zunächst deutlich steiler wächst als im Original, was jedoch für größere Ordinaten nachlässt. Die Funktion wird durch die Substitution im Bereich $0<x\leq 0.4$ auf ein schmaleres Intervall projeziert und dadurch wiederum gestaucht. Für größere $x$ wird die Funktion durch Substitution horizontal ausgedehnt. Man kann dieses Verhalten in Form einer Dichte (siehe ebenfalls Abbildung unten) visualisieren, indem man die Länge korrespondierender Abschnitte in beiden Graphen in der Form $\Delta x/\Delta y$ gegenüberstellt.

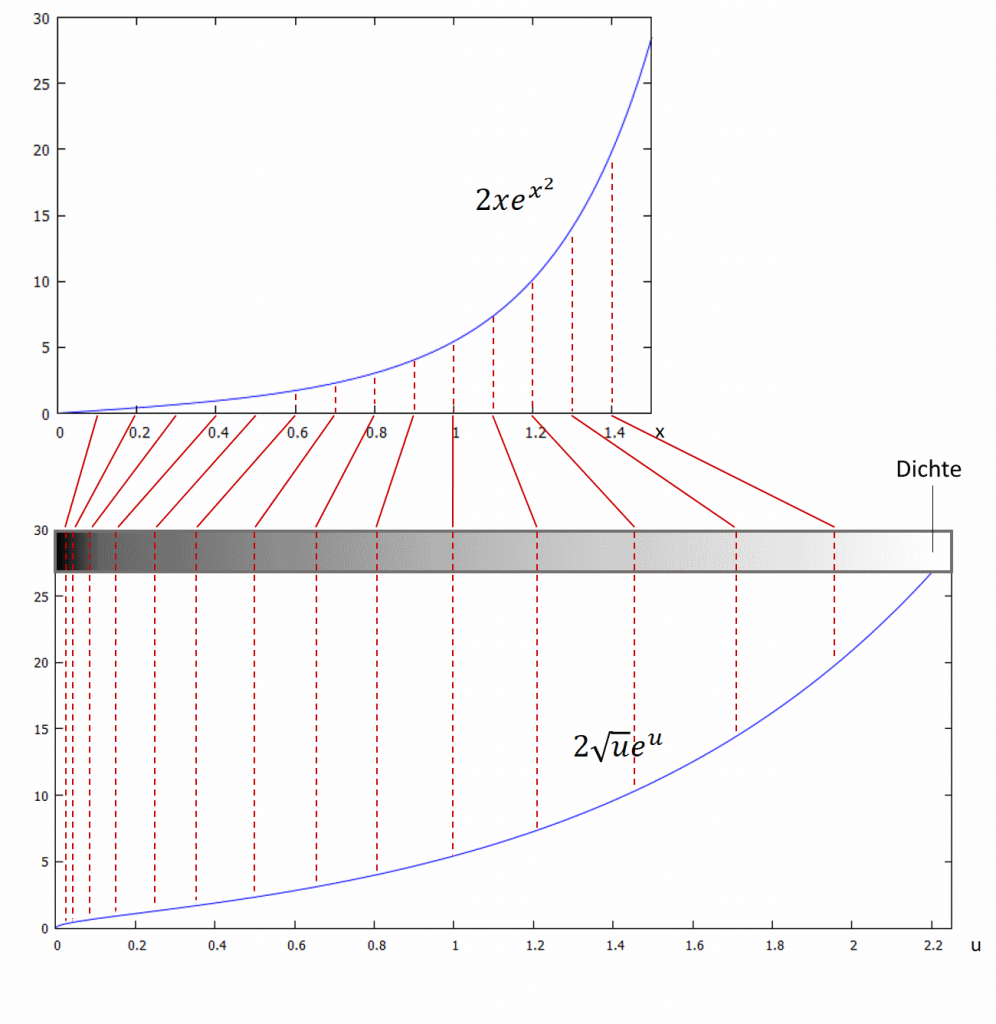
Integration durch Substitution kann die Form einer Funktion und deren Fläche unter Graphen massiv verändern. Substitution allein führt hier zum Fehler!

Durch horizontales Stauchen (hohe Dichte) wird die Funktion aber horizontal „kürzer“ und damit die Fläche unter der Kurve kleiner. Horizontales Strecken hingegen (geringe Dichte) führt zu einer künstlichen Vergrößerung der Fläche unter dem Graphen. Es gilt, eine nachträgliche Korrektur durchzuführen. In unserem Beispiel muss also für kleine $x$ Fläche unter dem Graphen der substituierten Funktion hinzugefügt werden und für größere $x$ umgekehrt. Der fehlende Faktor ist genau das Verhältnis $\Delta x/\Delta y$ , woraus im infinetsimalen Fall $dx/du$ wird. Daher,

$\displaystyle x'(u)=\frac{dx}{du}=\frac{d}{du} \left(\sqrt{u} \right)=\frac{1}{2\sqrt{u}}$

Und somit

$\displaystyle \int 2xe^{x^2}\, dx=\int 2\sqrt{u}e^{u} \left ( \frac{dx}{du}\right ) \, du$

$\displaystyle \int 2\sqrt{u}e^{u} \left ( \frac{dx}{du}\right ) \, du=\int 2\sqrt{u}e^{u} \frac{1}{2\sqrt{u}}\, du=\int e^{u} \, du$

$\displaystyle \int e^{u} \, du=e^{u}+c=e^{x^2}+c$

Viele Leute meinen nun $dx$ tatsächlich zu substituieren und stellen einfach entsprechend um (was eine sehr gute Eselsbrücke ist):

$\displaystyle \frac{dx}{du}=\frac{1}{2\sqrt{u}} \iff dx=\frac{1}{2\sqrt{u}}$

Manchmal ist es auch einfacher, die Umkehrung $du/dx$ abzuleiten. Durch Reflektion an $y=x$ und Rück-Substitution ergibt sich dann das gleiche Ergebnis:

$\displaystyle \frac{dx}{du}= \frac{1}{\frac{du}{dx}} \iff dx=\frac{1}{2\sqrt{u}}$

Ein abschließendes Beispiel

Um den Beitrag abzurunden, möchte ich noch ein gesamtheitliches Beispiel liefern, welches illustriert, dass Integration durch Substitution nur selten allein daher kommt. Eine weitere nützliche Technik ist die partielle Integration, welche auf der Umkehrung der Produktregel der Differenzialrechnung beruht. Zudem werden wir in diesem Beispiel nicht zurücksubstitutieren, sondern ein bestimmtes Integral (also mit Grenzen) berechnen. Auf geht’s!

$\displaystyle A=\int\limits_{0}^{1} e^{\sqrt{x+1}}\, dx$

Mithilfe der Substitution $u=\sqrt{x+1}$ für die Grenzen des Integrals und $x(u)=u^{2}-1$ für die Funktion selbst vereinfacht sich das Integral wie folgt.

$\displaystyle A=\int\limits_{\sqrt{0+1}}^{\sqrt{1+1}} e^{\sqrt{(u^{2}-1)+1}}\, dx$

Die Anwendung der Eselsbrücke ergibt $dx=x'(u)\, du=2u\, du$ und damit:

$\displaystyle A=\int\limits_{1}^{\sqrt{2}} e^{u}\times 2u \, du$

An dieser Stelle kommt die partielle Integration ins Spiel:

$\displaystyle A=\left[e^{u}\, 2u \right]_{1}^{\sqrt{2}}- \int\limits_{1}^{\sqrt{2}} e^{u}\times 2 \, du=\left[2u\, e^{u} - 2e^{u}\right]_{1}^{\sqrt{2}}$