Bei den vielen Abartigkeiten des Straßenverkehrs rangiert das Thema „Parken“ ganz weit oben. Oft frage ich mich, was einigen Autofahrern durch den Kopf geht, wenn sie ihr Gefährt einfach irgendwo schief fallen lassen. Dieser Beitrag soll sich jedoch nicht mit den eigentümlichen Gewohnheiten einzelner Fahrer beschäftigen. Es geht um die Grunsatzfrage: Markierter Stellplatz oder nicht? Was ist sinnvoller?
Die Natur beider Varianten
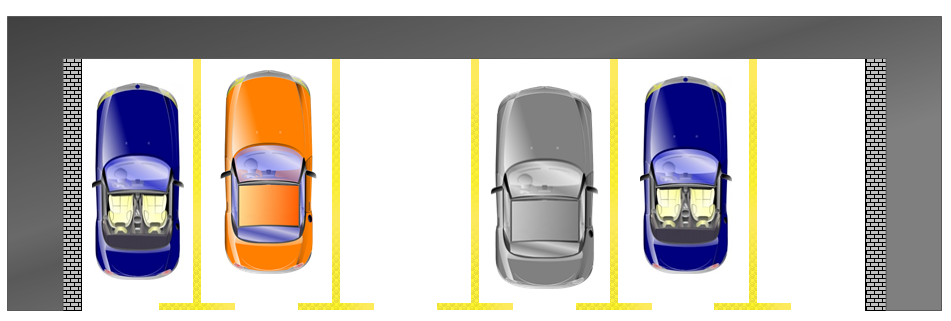
Modell 1 ist der klassische Stellplatz. Charakteristisch ist, dass je ein PKW in eine Lücke passt. Die Zahl der Parkplätze ist vorgegeben, nur der Abstand zwischen zwei benachbarten PKWs ist von deren Breite abhängig. Wer ein großes Auto fährt, hat also weniger Platz zum Aussteigen – klingt fair.
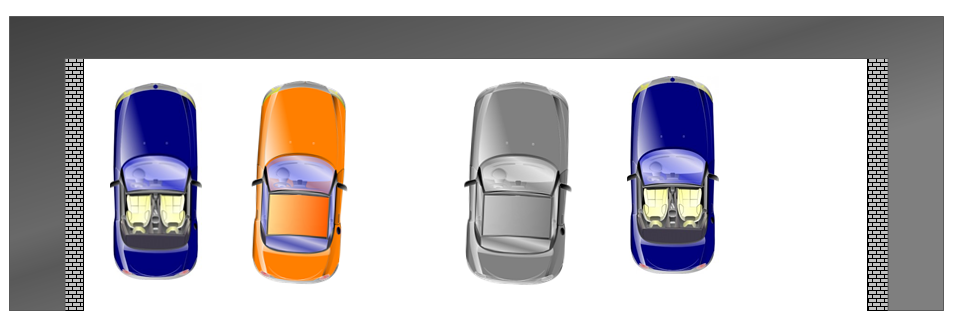
Modell 2 sind flexible Parkplätze. Wir werden uns deren Eigenschaften später noch genauer ansehen. An dieser Stelle sei darauf hingewiesen, dass fehlende Markierungen zum schiefen Einparken verleiten. Viel interessanter ist jedoch der Umstand, dass sich mit der Zeit relativ große Lücken zwischen den Autos bilden. Dies liegt nicht zwingend am mangelnden Können der Fahrzeugführer. Es kommt einfach häufig vor, dass ein breiter Wagen ausparkt und die Lücke anschließend von einem schmaleren gefüllt wird. Mit der Zeit ergibt sich ein Bild wie in der Abbildung unten.
Falsche Vorstellungen
Der Stellplatz-Kritiker argumentiert nun damit, dass die Flexibilität Modell 2 viel platzschonender macht. Also vergleichen wir – beginnend mit dem einfachen Modell 1. Angenommen, die Breite eines Stellplatzes betrage 2,50m, und weiterhin angenommen, dass die durchschnittliche Breite eines PKWs 1,70m beträgt; dann beträgt der durchschnittliche Abstand zwischen zwei Autos . Setzen wir diesen Abstand in die Berechnung für Modell 2 ein: Wenn jeder PKW 80cm neben dem anderen parkt, dann ist der benötigte Platz für 10 PKW im Durchschnitt identisch zu Modell 1 (falls wir weiterhin mit einer durchschnittlichen Fahrzeugbreite von 1,70m kalkulieren).
Besteht also kein Unterschied zwischen beiden Modellen? Doch! Der Unterschied wird offenkundig, wenn man Modell 2 exakter berechnet. Nehmen wir neben der Fahrzeugbreite von 1,70m zusätzlich an, dass die Fahrzeugbreite normalverteilt und 2/3 der Fahrzeuge zwischen 1,60m und 1,80m breit sind (die Annahme wird von der Zulassungsstatistik gestützt). Der Abstand der gewählten Grenzen zum Erwartungs- bzw. Mittelwert 1,70m beträgt in diesem Fall . Der benötigte Gesamtabstand
für
Fahrzeuge lässt sich durch Addition der Abstände sowie der Breite
berechnen:
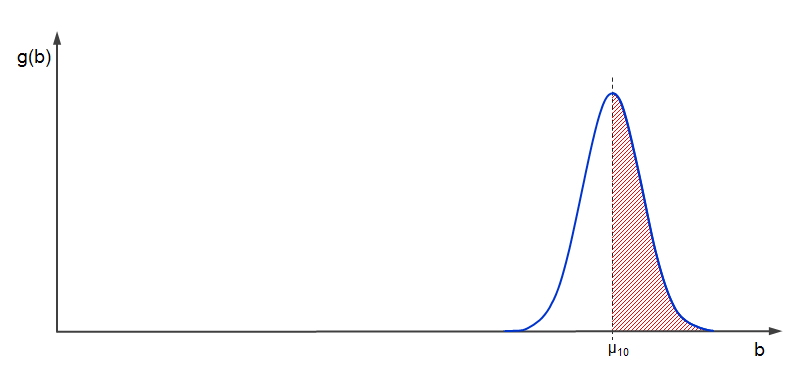
Für 10 Fahrzeuge ergibt sich die nachfolgende Verteilung für . Der Denkfehler des Kritikers fester Parklücken besteht darin, dass er nur den positiven Fall, in welchem Platz verfügbar wird, betrachtet. Aber sobald die Autos einmal überdurchschnittlich breit werden, passen nicht mehr alle 10 Fahrzeuge in die verfügbaren 25m. Die Wahrscheinlichkeit hierfür beträgt satte 50%!
Bleibt noch die Berechnung für den positiven Fall. Durch Addition der Varianzen jedes einzelnen Fahrzeuges können wir die Standardabweichung der resultierenden Verteilung für 11 Fahrzeuge ermitteln. Wir müssen nun einfach die Wahrscheinlichkeit dafür bestimmen, dass der benötigte Platz geringer als 25m ist. Die Grafik unten illustriert das.
Allerdings übertreibt die Grafik die Wahrscheinlichkeit. Mit R habe ich schnell ausgerechnet, dass die Wahrscheinlichkeit quasi 0 ist!
> pnorm(25,mean=27.5,sd=sqrt(11*0.1^2),lower.tail=TRUE) [1] 2.390131e-14
Nur mal so nebenbei: Damit man auch nur annähernd auf eine Wahrscheinlichkeit von 4% für zusätzliche Autos auf einer Parkfläche kommt, müsste man in unserem Szenario 200 Autos auf einer Breite von 500m nebeneinander stellen. Das ist jedoch utopisch…
Fazit
Die Idee des flexiblen Parkens benachteiligt offensichtlich mit hoher Wahrscheinlichkeit einzelne Fahrzeuge. Vorgezeichnete Parklücken hingegen gewähren einer festen Zahl von Parkplatzsuchenden Raum. Sie strafen überbreite Fahrzeuge ab und lassen schmalen Fahrzeugen Raum. Damit sind sie die bessere Wahl – fast immer! Wir sind von einer Breite von 2,50m ausgegangen; gesetzlich vorgeschrieben sind in den Garagenverordnungen der Länder i. d. R. mindestens 2,30m. Wählt man die Abstände größer, verschwendet man jedoch Platz. Sollte man auf die Idee kommen, mehr Parkplätze schaffen zu können, indem man die Lücken schmaler macht, dann führt das zu einem klassischen Rebound-Effekt. In diesem Falle würden die Markierungen ihre Wirkung verlieren. Wie in diesem Beitrag erörtert wurde, wird die mögliche Anzahl von Fahrzeugen auf dem Parkplatz dadurch aber reduziert 😉
Find a description of the statistics behind the physics of parking spaces 🙂


 (2 Stimmen, Durchnschnitt: 4,50 von 5)
(2 Stimmen, Durchnschnitt: 4,50 von 5)





30. Dezember 2015 at 7:55
Und dann gibt es noch die Hutfahrer, die grundsätzlich 2 Stellplätze verparken, ob markiert oder nicht.
14. Februar 2016 at 11:41
Erstaunlicherweise scheint die Einparkfähigkeit negativ mit der Fahrzeugbreite zu korrelieren. Die Fahrer der dicken SUV sind auch meist zu doof zum parken und brauchen selbst dann zwei Parkplätze, wenn eigentlich genug Platz wäre.
14. Februar 2016 at 12:02
Aus meiner Erfahrung heraus wird da einfach an der falschen Stelle gespart: Den Qashqai meiner Frau kann jeder dank 4 Kameras und 360°-Vorgelperspektivensicht kinderleicht einparken 🙂