Vitamin D ist an vielen Prozessen im menschlichen Körper beteiligt. In nördlichen Ländern bildet der Körper in den Wintermonaten (Okotober-März) kaum Vitamin D, weil die die dazu benötigte UV-B-Strahlung aufgrund des Einfallswinkels des Lichts in der Atmosphäre herausgefiltert wird (siehe dieser Beitrag) . Da spielt es auch keine Rolle, wie lange man sich in der Sonne aufhält. Um mit der Nahrung genügend Vitamin D zu sich zu nehmen, muss supplementiert werden. Die Empfehlung liegt für Erwachsene bei 600 IE (Institute od Medicine) bzw. 800 IE (Deutsche Gesellschaft für Ernährung) Vitamin D3. Der Clou: Ein seit 2014 existierender Review zeigt, dass die Empfehlung wegen eines Rechenfehlers zehnmal so hoch sein müsste. Dass die meisten Menschen davon keine Notiz nehmen, liegt wohlmöglich an der zugrunde liegenden, komplizierten Statistik. Dieser Beitrag versucht, Abhilfe zu schaffen.
Wie die Empfehlung für die Gabe von Vitamin D berechnet wurde
Zur Ermittlung der empfohlenen Tagesdosis untersuchten die Forscher verschiedene bereits existierende Studien, welche vorranging an Probanten in nördlichen Ländern durchgeführt wurden. Jede einzelne dieser Studien gab Aufschluss über die Wirkung spezieller Dosen Vitamin D3 (nachfolgend einfach Vitamin D genannt). Man kann in diesen Studien erkennen, wie viel Prozent der Probanten (stellvertretend für die gesamte Population; also die Bevölkerung) welchen Vitamin-D-Spiegel unter Gabe einer bestimmten Dosis erreichen. In der Grafik unten sehen wir eine solche beispielhafte Verteilung als qualitative Darstellung. Zudem habe ich sowohl eine Unter- wie auch Obergrenze eingetragen. Die Forscher wählten insbesondere die Untergrenze so, dass 2,5% der Probanten darunter liegen (in der Fachsprache auch 2,5%-Quantil bzw. 0,025-Qunatil genannt). Dies wird später noch wichtig.
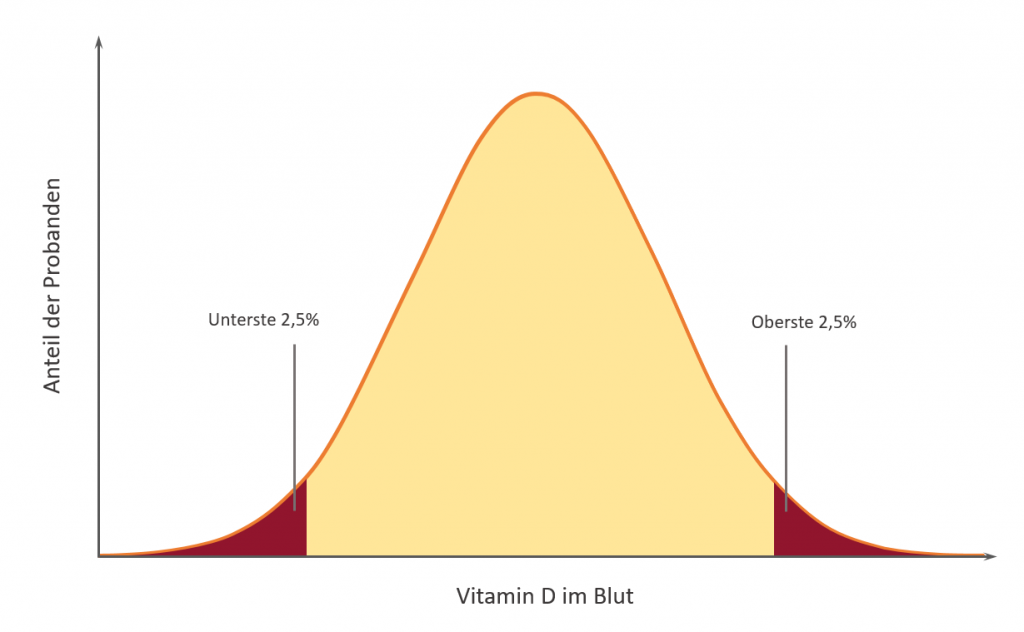
Die Gabe einer spezifischen Dosis führt bei verschiedenen Menschen zu unterschiedlichem Anstieg des Vitamin D im Blut
Wenn man die Daten nun geschickt miteinander kombiniert, dann lässt sich eine solche Verteilung für eine Vielzahl an Dosen ermitteln und in einem Diagramm auftragen. Unten habe ich dies (wieder deutlich vereinfacht) getan. Auf der horizontalen Achse ist die wachsende Dosis aufgetragen, während der Vitamin-D-Spiegel vertikal verzeichnet ist. Zudem habe ich für jede Dosis die Beispielverteilung von oben eingezeichnet. Mittels Regression entsteht ein kontinuierliches, mathematisches Vorhersagemodell, welches auch Aussagen über den Verlauf der gewählten Grenzen erlaubt. Vor allem die untere 2,5%-Grenze war für die Forscher interessant. Erreicht der Blutspiegel bereits an dieser Grenze die empfohlenen 50 nmol/l (20 ng/ml), dann sind folglich 97,5% der Bevölkerung mit der zugehörigen Dosis mindestens ausreichend versorgt. Der Schnittpunkt in der Grafik markiert daher die empfohlende Tagesdosis.
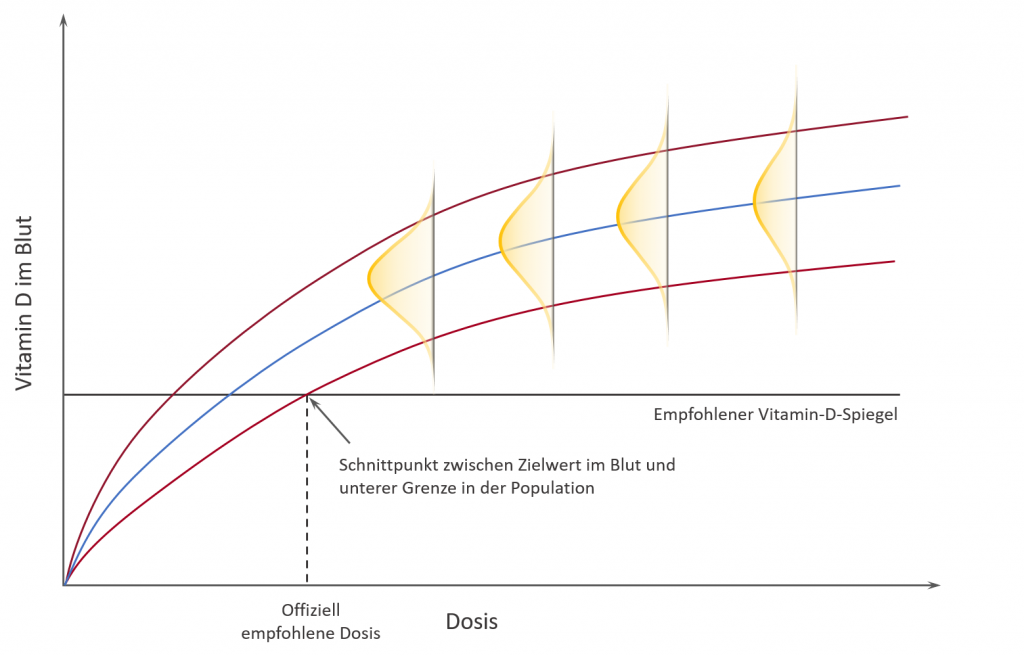
Für verschiedene Dosen ergibt sich eine Kurve, welche den Zusammenhang zwischen Dosis und Blutspiegel des Vitamins D beschreibt. 2,5% landen bei gegebener Dosis unterhalb der unteren roten Linie.
Unter realen Daten ergibt sich nach diesem stark vereinfacht dargestellten Verfahren eine empfohlene Tageszufuhr von 600 IE (Internationale Einheiten) Vitamin D.
Ein Rechenfehler drückt die empfohlene Dosis
Um zu erklären, wo genau im oben erläuterten Verfahren der Fehler liegt, müssen wir einen kleinen Exkurs machen. Meine hierfür gewählte Würfel-Simulation umfasst tausend Durchgänge, in denen jeweils einmal gewürfelt wurde. In der Grafik unten sehen wir zunächst eine Gleichverteilung (oben links) für dieses einfache Würfeln. Würfelt man hingegen in jedem Durchgang zweimal und bildet den Durchschnitt der beiden Augenzahlen, dann ergibt sich eine Häufigkeitsverteilung wie oben rechts dargestellt. Der Wert 3,5 ist dabei natürlich am häufigsten, weil man ihn aus vielen Kombinationen (1+6, 2+5 und 3+4) bilden kann, während es für die äußeren Werte 1 und 6 jeweils nur die Kombination 1+1 und 6+6 gibt.
Wird in jedem der 1000 Durchgänge 20-mal gewürfelt, dann wird die Häufigkeitsverteilung enger (unten links) und nähert sich deutlich einer Normalverteilung an. Für 100-mal Würfeln wird die Verteilung nochmals enger. Es ist leicht, sich jeden der 1000 Durchgänge als einzelne Studie vorzustellen. Je größer die Studie (also je größer n in der Grafik) desto kleiner fällt die Varianz aus und die Verteilung erscheint entsprechend enger.
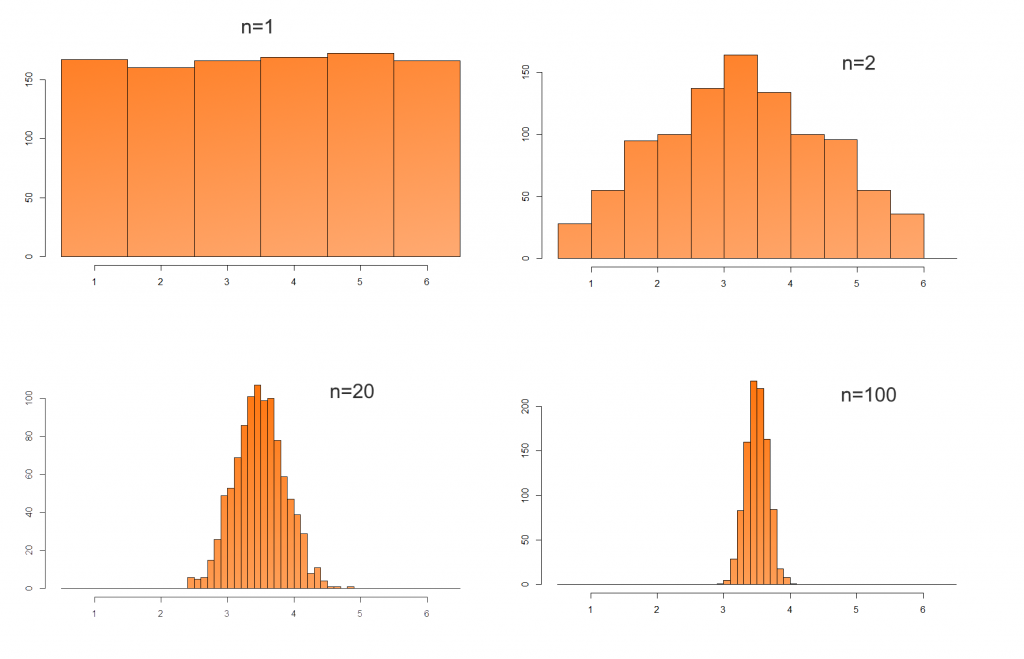
Beispiel: Beim Würfeln entsteht eine Gleichverteilung (n=1). Würfelt man zweimal und bildet den Mittelwert, dann ist die Wahrscheinlichkeit für einen Wert um 3.5 größer als für 1 oder 6 (n=2). Würfelt man jeweils 20 oder gar 100 mal, dann stellt sich einer immer schmaler werdende Normalverteilung für die Mittelwerte ein.
Nun ist den Forschern folgender Fauxpas unterlaufen: Anstatt die zugrundeliegenden Daten der Studien für ihr Modell zu verwenden, griffen sie auf die im Mittel erreichten Blutspiegel je Studie und Dosis zurück. Die Verteilung ist dann vergleichbar mit der Abbildung für n=100. Zur Bestimmung einer aussagekräftigen unteren Grenze bei 2,5% der Bevölkerung hätten sie jedoch auf Daten für jedes Individuum zurückgreifen müssen; vergleichbar mit n=1 in der oben gezeigten Abbildung. Die Verteilung der Forscher war dadurch zu schmal und die 2,5%-Grenze in Folge zu groß gewählt. Im korrekten Modell müssten die Grenzen entsprechend weiter gefasst werden:
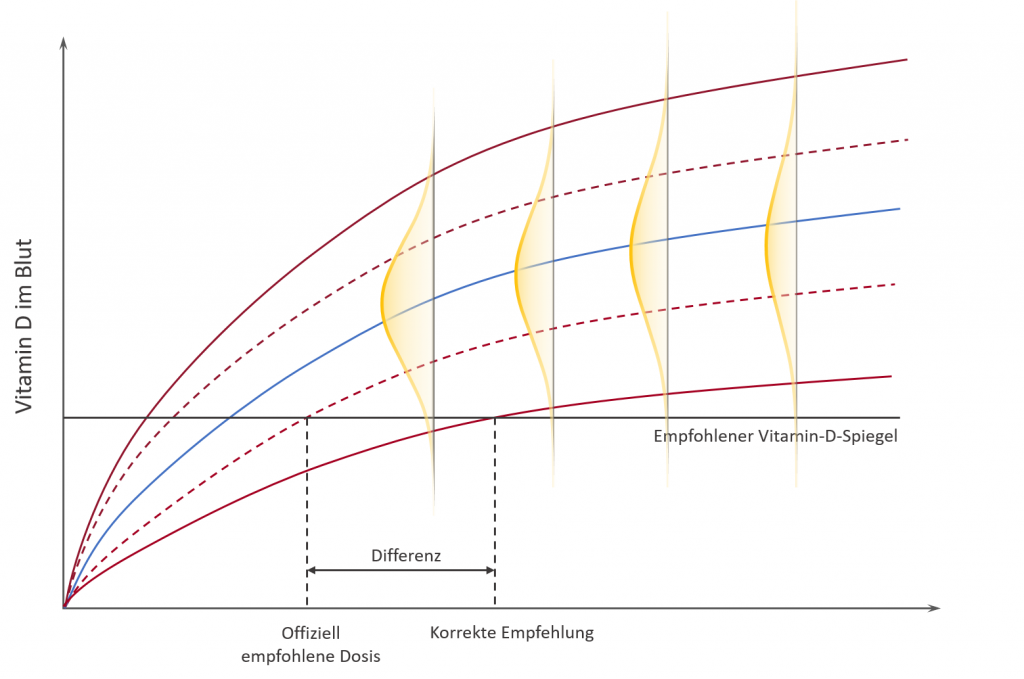
Die symbolhafte untere Grenze, welche auf Mittelwerten beruhte, ist gestrichelt dargestellt. Die neue untere Grenze, welche wirklich nur 2,5% der Bevölkerung unterschreiten, ist als rote Linie dargestellt. Alter und neuer Schnittpunkt mit dem empfohlenen Vitamin-D-Spiegel weisen auf eine Differenz hin.
Da die untere Grenze nun erst bei höherer Dosis den empfohlenen Vitamin-D-Spiegel trifft, verschiebt sich die empfohlene Tagesdosis entsprechend. In der Grafik sieht das nicht so gravierend aus, was aber an der vereinfachten Darstellung meinerseits liegt. Der Review der realen Daten hat ergeben, dass sich die empfohlene Tagesdosis von 600 IE auf 6000 IE ändert!
Auswirkungen
Ich selbst wies im Frühjahr 2017 einen Vitamin-D-Spiegel von nur 21 ng/ml auf. Festgestellt wurde dies, als ich längere Zeit krank war. Im folgenden Winter hielt ich mich an die 6000 IE/Tag und konnte dank Vitamin D3 des Herstellers Pure meinen Blutspiegel auf 30 ng/l steigern. Einen solchen Test (beispielsweise vom Anbieter Cerascreen) kann übrigens jeder selbst nach Hause bestellen. Ein Wert von 30 ng/l gilt zwar als ausreichend, ist aber vom oft genannten Idealwert 50 ng/ml noch weit entfernt.
Mein persönliches Beispiel zeigt, dass 600 IE viel zu wenig gewesen wären, um einen nennenswerten Anstieg des Vitamin-D-Spiegels herbeizuführen. Wer an einem Mangel leidet, muss der Nahrung kräftig zumischen. Das ist auch nicht unnatürlich, wenn man bedenkt, dass die Menschheit für die winterliche Sonnenarmut in Nordeuropa gar nicht ausgelegt ist. Nichtsdestotrotz sollte man regelmäßig und lange in die Sonne gehen. Sie erfüllt schließlich noch weitere Zwecke; beispielsweise als Signal für den Tag-Nacht-Zyklus.

 (23 Stimmen, Durchnschnitt: 4,48 von 5)
(23 Stimmen, Durchnschnitt: 4,48 von 5)




Schreibe einen Kommentar