Der systematisch unterschätzte Luftwiderstand

Inhalt

Das Gedankenexperiment
Die Physik
Das Beispiel
Das Fazit

Als ich vor wenigen Tagen einige Vorurteile über SUVs aus der Welt räumte, fühlte ich mich leicht geläutert. Durch ihre enorme Querschnittsfläche und teilweise etwas schlechteren cw-Werte weisen SUVs einen höheren Verbrauch auf als Fahrzeuge einiger anderer Segmente. Wie ich so über den Luftwiderstand nachdachte, ist mir ein interessanter Gedanke gekommen: Welchen Einfluss hat eigentlich der Wind bei einer Autofahrt auf den Luftwiderstand?

Das Gedankenexperiment

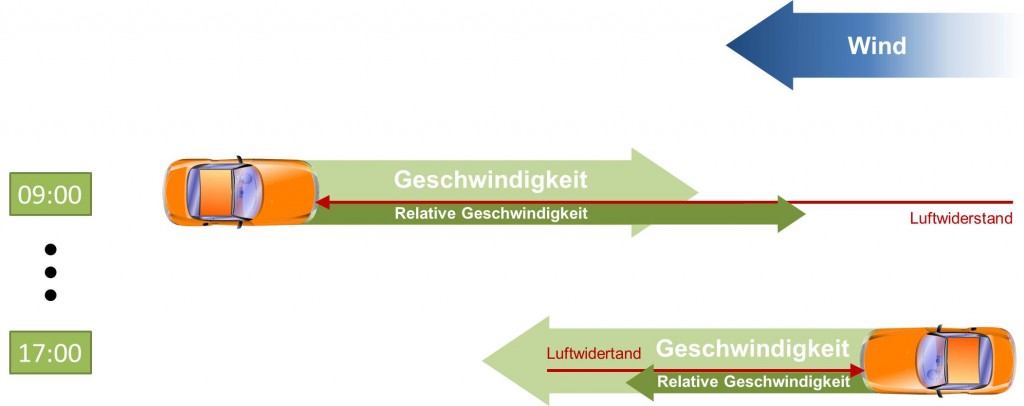
Mein erster Impuls trieb mich zur Annahme, dass sich der Einfluss des Windes herausmittelt; schließlich hat man den Wind nur in einer Richtung gegen sich – auf dem Rückweg unterstützt einen der Wind ja quasi von hinten. Allerdings ist es auch so, dass der Luftwiderstand mit der Fahrtgeschwindigkeit quadratisch zunimmt. Es kommt also auf die relative Geschwindigkeit im Vergleich zum Wind an!

Physikalische Größen bei Fahrt mit und gegen den Wind

Die Physik

Man kann das auch sehr schön aus der Theorie herleiten. Der Luftwiderstand wird mit folgender Formel berechnet:

$\displaystyle F_{L}=\frac{A\cdot\varrho \cdot v^{2}\cdot c_{w}}{2}$

Außerdem können wir als Funktion der Windgeschwindigkeit schreiben:

$\displaystyle F_{L}(v_{w})=\frac{A\cdot\varrho \cdot (v+v_{w})^{2}\cdot c_{w}}{2}$

Möchten wir nun den mittleren Unterschied zum Luftwiderstand ohne Wind errechnen, bilden wir die Differenz beider Luftwiderstände und teilen durch zwei. Für $v\geq 0$ erhalten wir:

$\displaystyle \overline{\Delta F_{L}(v_{w})}=\frac{F_L(v_{w})-F_L(-v_{w})}{2}$

$\displaystyle \overline{\Delta F_{L}(v_{w})}=\frac{A\cdot\varrho \cdot (v+v_{w})^{2}\cdot c_{w}-A\cdot\varrho \cdot (v-v_{w})^{2}\cdot c_{w}}{4}$

$\displaystyle \overline{\Delta F_{L}(v_{w})}=\frac{A\cdot\varrho \cdot c_{w} }{4}\big((v+v_{w})^{2}-(v-v_{w})^{2}\big)$

$\displaystyle \overline{\Delta F_{L}(v_{w})}=\frac{A\cdot\varrho \cdot c_{w} }{4}\big(4\cdot v\cdot v_{w}\big)=A\cdot\varrho \cdot c_{w}\cdot v\cdot v_{w}$

Damit können wir doch rechnen!

Das Beispiel

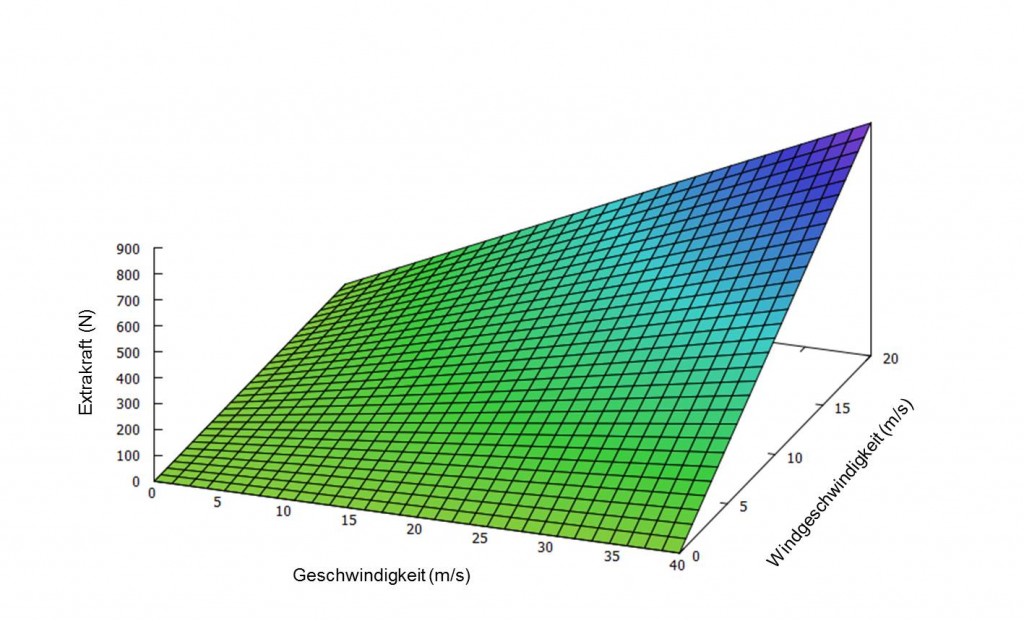
Für verschiedene (Wind)geschwindigkeiten ergeben sich unterschiedliche durchschnittliche Zusatzkräfte, die da wirken. Die folgende Grafik illustriert den Mehrbedarf.

Zusätzlich benötigte Kraft bei Fahrten im Wind

Man muss nun noch berücksichtigen, dass pro 100N etwa 0,8 Liter mehr Benzin pro 100km verbraucht werden. Wer also mit 120km/h bei einen moderaten Wind von 20km/h fährt, verbraucht im Schnitt bis zu 1,6 Liter mehr auf 100km. Das ist doch eine ganze Menge!

Das Fazit

Ich lese nicht oft Auto-Zeitschriften. In der Regel staune ich jedoch darüber, welch absonderliche Spritspar-Maßnahmen zum Teil propagiert werden, um 10ml Sprit auf 100km zu sparen. Das war jetzt vielleicht etwas übertrieben… Dennoch ist es seltsam, dass etablierte Formate wie „AutoBild“ & Co. überhaupt nicht auf diesen heftig wirkenden Effekt eingehen. Aber auch beim Googlen durchs Netz, erhärtete sich bei mir der Eindruck, die meisten Menschen hätten sich mit den Parametern Geschwindigkeit, cw-Wert und Stirn-/Querschnittsfläche als Treiber des Luftwiderstandes abgefunden.

Wie wir gesehen haben, ist der Einfluss des Windes auf den mittleren Luftwiderstand aber nicht unerheblich und vor allem praktisch immer existent. Selbst Böen könnten den mittleren Luftwiderstand extrem anheben. Meine persönliche Lieblingsüberlegung ist seit ein paar Minuten die Frage, ob man an der windigen See im Schnitt mehr Sprit verbraucht als in mitteldeutschen Gegenden… 😀 Auf jeden Fall habt ihr jetzt einen weiteren Grund zuhause zu bleiben, wenn es in den nächsten Monaten wieder stark zu winden beginnt.

Find an explanation of the relationship between wind strength and fuel consumption in English >>

2 Kommentare

Ulrich Koletzki
15. Februar 2022 at 11:42

Mir scheint, drei Formeln enthalten einen Fehler. Es sollte doch durch 2 geteilt werden und nicht durch 4.

Antworten
- Jan Rothkegel (Beitrag Autor)
  16. Februar 2022 at 17:43
  
  Hallo Ulrich,
  
  danke für deine Antwort. Die Division durch vier rührt daher, dass wir die Differenz der Luftwiderstände noch einmal durch zwei dividieren. Ich habe zwei Zwischenschritte eingefügt, die den Sachverhalt hoffentlich transparenter machen.
  
  Liebe Grüße
  Jan
  
  Antworten