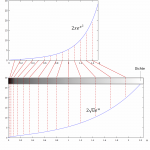
Früher hatten die Menschen wohl noch Zeit, um sich den wirklich interessanten Fragen des Alltags zu stellen. Thomas M. Cover stieß beispielsweise auf das Phänomen des Zwei-Zettel-Spieles. Die Idee ist simpel: Man nehme zwei Zettel und lasse von einer Person zwei zufällige (und sinnvollerweise auch unterschiedliche) Zahlen darauf schreiben. Nun darf man einen der beiden Zettel wählen. Nach Betrachtung der darauf notierten Zahl, muss man einen Tipp darüber abgeben, ob die Zahl auf dem anderen Zettel größer oder kleiner ist. Da es sich um beliebige Zahlen handeln kann, müsste die Wahrscheinlichkeit für einen korrekten Tipp bei 50% liegen. Tatsächlich gibt es aber eine Strategie, die mindestens 50% Trefferwahrscheinlichkeit erzielt. Es gibt Dinge, die sind schon verblüffend! Lesen Sie weiter →
Was die Welt im Innersten zusammenhält
Ein wissenschaftlicher Blog über die verblüffenden Zusammenhänge der Welt
Schlagwort: Statistik (page 2 of 2)
Bei den vielen Abartigkeiten des Straßenverkehrs rangiert das Thema „Parken“ ganz weit oben. Oft frage ich mich, was einigen Autofahrern durch den Kopf geht, wenn sie ihr Gefährt einfach irgendwo schief fallen lassen. Dieser Beitrag soll sich jedoch nicht mit den eigentümlichen Gewohnheiten einzelner Fahrer beschäftigen. Es geht um die Grunsatzfrage: Markierter Stellplatz oder nicht? Was ist sinnvoller? Lesen Sie weiter →
Viele Menschen verwenden ja Regeln, die garnicht mehr hinterfragt werden. Beispielsweise dürfen Varianzen unabhängiger Zufallsvariablen direkt addiert werden, sofern die Zufallsvariablen unabhängig sind. Die Begründung für diesen Umstand weiß man dann oft nicht so genau. Daher möchte ich hier die Herleitung der Regel kurz skizzieren. Vielleicht hilft es euch, im Vorfeld zu lesen, warum man Erwartungswerte addieren und multiplizieren kann. Lesen Sie weiter →
Wer schon einmal mit diskreten Zufallsvariablen zu tun hatte, der weiß, dass man den Erwartungswert manchmal vor lauter Summenzeichen nicht mehr erkennt 🙂 In der Regel kommt man in der Welt der kontinuierlichen Statistik deutlich schneller ans Ziel. Daher zeige ich heute, wie man den Erwartungswert einer diskreten Zufallsvariable über die analoge kontinuierliche Verteilung nähern kann. Lesen Sie weiter →
© 2024 Was die Welt im Innersten zusammenhält
Theme by Anders Noren — Up ↑