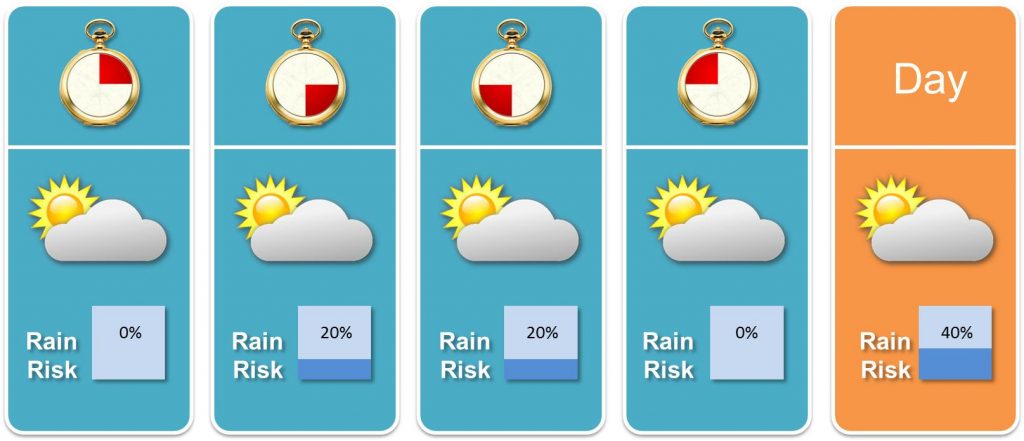
Es geht wieder in großen Schritten auf die dunkle Jahreszeit zu – und Stück für Stück steigt das Regenrisiko. Wer empfindliche Kleidung tragen will, schaut daher lieber in den Wetterbericht. Dabei wird der eine oder andere sicher bereits festgestellt haben, dass die Niederschlagswahrscheinlichkeit inzwischen sehr detailliert (bis auf die Stunde genau) angegeben wird. Bedeutung und Zusammenhang zwischen der groben täglichen Niederschlagswahrscheinlichkeit und ihren feineren Abstufungen geben dabei vielen Mitmenschen Rätsel auf. Nehmen wir folgendes Beispiel vom Schwesternblog Insight Things her:
Was sagt uns das Regenrisiko/Niederschlagswahrscheinlichkeit ganz generell? Und wie kommt man von 2 mal 20% Regenwahrscheinlichkeit auf 40% für den ganzen Tag? Diese Fragen werde ich im Folgenden beantworten!
Definition der Niederschlagswahrscheinlichkeit
Eine sehr einfache Definition gibt der Deutsche Wetterdienst (DWD) an. Demnach wird einfach auf vergleichbare Wetterkonstellationen der Vergangenheit geschaut und die Niederschlagswahrscheinlichkeit als relative Häufigkeit angegeben. Eine Niederschlagswahrscheinlichkeit von 40% sagt demnach aus, dass es in 4 von 10 Fällen der Vergangenheit zu Niederschlag (Regen, Graupel, Schnee) im Zielgebiet kam und dort demnach auch in Zukunft an 4 von Tagen zu Niederschlag kommen wird.
Der amerikanische Wetterdienst fasst sich beim Konzept der Probability of Precipitation (POP) etwas konkreter und gibt sogar eine Formel an. In dieser Formel taucht beispielsweise eine Flächenabdeckung auf – also ein Prognosewert hinsichtlich der Fläche, auf der es im Zielgebiet regnen soll. Auch die Niederschlagsmenge, welche als Regen gelten soll, ist genau definiert.
Noch ein Wort zu den historischen Niederschlagsdaten: Die Daten über vergangene Niederschläge heranzuziehen ist sicher eine solide Möglichkeit. Nichtsdestotrotz werden Meteorologen auch chaotische Wettermodelle abfahren und durch Variation der Parameter Szenarien generieren. Auch auf diesem Weg lassen sich relative Häufigkeiten generieren. Für meine weiteren Erläuterungen ist dies aber nicht von Bedeutung.
Detailliertes Regenrisiko
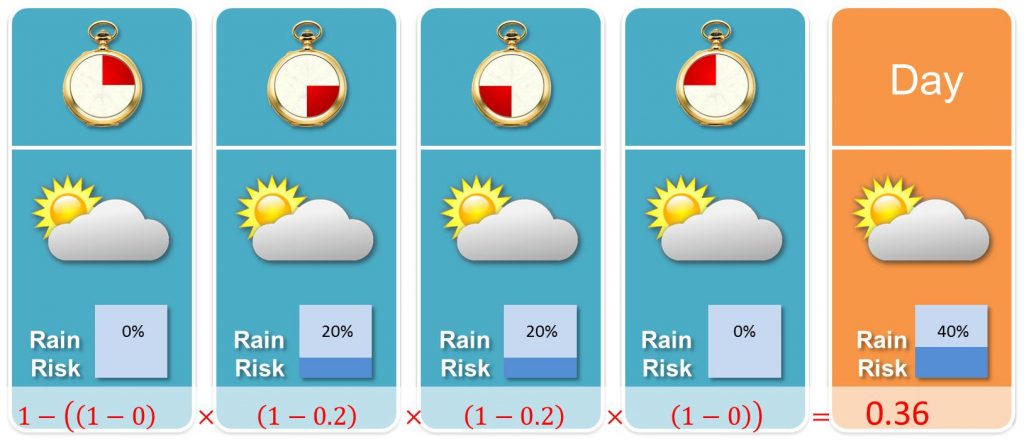
Wie bereits erwähnt, wird die Niederschlagswahrscheinlichkeit inzwischen recht detailliert dargestellt. Wer bereits mit Stochastik zu tun hatte, dem wird auffallen, dass die Einzelwahrscheinlichkeiten nur schwer mit der Niederschlagswahrscheinlichkeit eines gesamten Tages in Einklang zu bringen sind. Durch Multiplikation der Wahrscheinlichkeiten der Gegenereignisse („Es regnet nicht.“) würden wie etwa folgende Tageswahrscheinlichkeit erhalten:
Der Unterschied zwischen den theoretischen 36% und den prognostizierten 40% beträgt aber immerhin 4 Prozentpunkte. Woher kommt das?
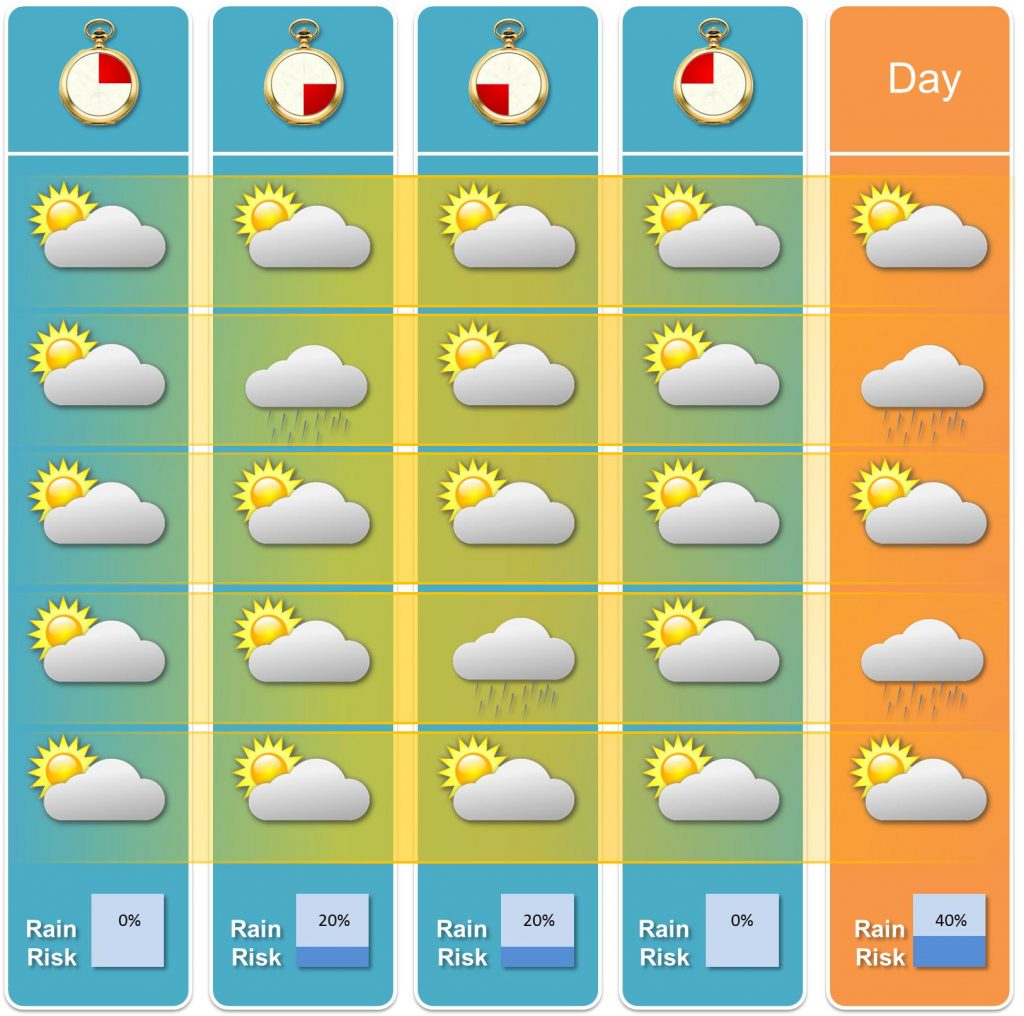
Wenn wir uns an die Definition der Niederschlagswahrscheinlichkeit zurückerinnern, finden wir die Auflösung. Man nehme historische oder simulierte Daten und bilde dann einmal die relative Häufigkeit zu den einzelnen Tageszeiten und für den gesamten Tag. Das könnte beispielsweise so aussehen:
Wie man gut erkennt, könnten die gezeigten Prognosewerte auf Basis dieser Daten tatsächlich erhalten worden sein. Nachdem man dieses konstruierte Beispiel gesehen hat, wird ersichtlich, dass eine Verknüpfung der einzelnen Ereignisse eines Tages zur Gesamtwahrscheinlichkeit so direkt nicht möglich ist. Vielmehr muss jedes Aggregationsniveau (Stunde, Tag, Monat, …) für sich betrachtet werden.
Stochastische Interpretation der Niederschlagswahrscheinlichkeit
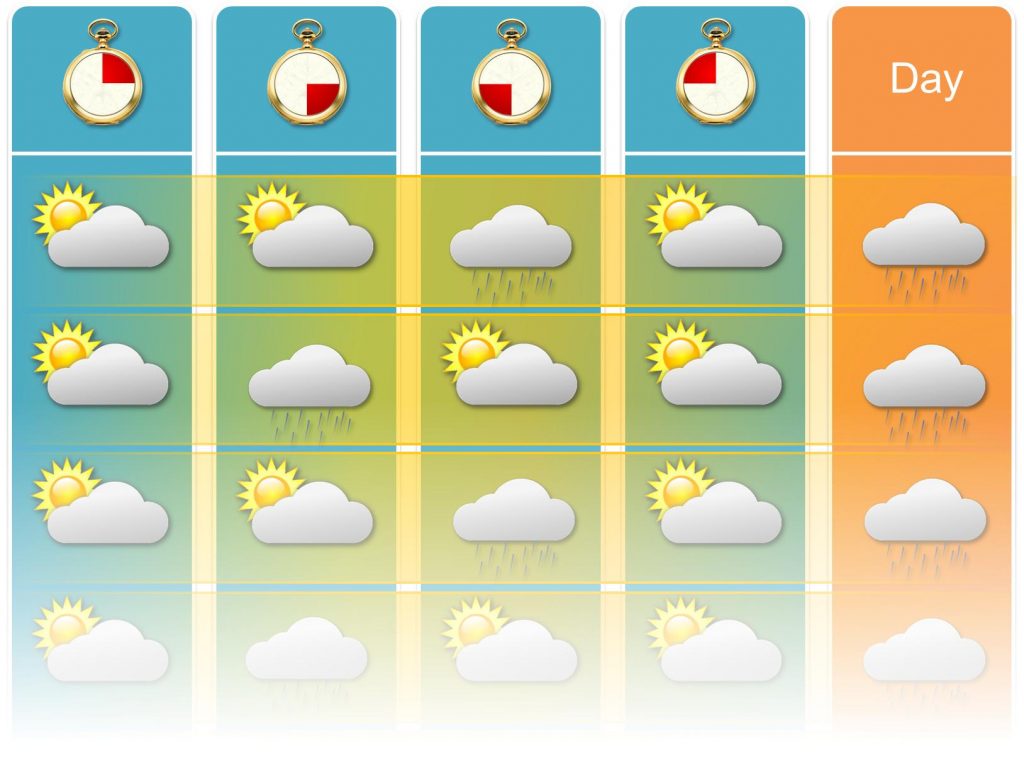
Tatsächlich ist die Wahrscheinlichkeit, dass sich zu einer bestimmten Tageszeit Niederschlag einstellt, nicht unabhängig. Sie können sogar in ziemlich starker Korrelation zueinander stehen. Man beachte nachfolgendes Beispiel.
In jedem Fall scheint es zu einer Zeit zu regnen – zur anderen jedoch nicht. Wir erhalten also zweimal 50% Niederschlagswahrscheinlichkeit. Wen also interessiert, ob er besser vor oder nach 6:00 zur Arbeit gehen soll, dem hilft die Information einer 50:50 Regenwahrscheinlichkeit eher nicht. Ihm würde nur die abgeleitete Regel helfen („Wenn es vor 6:00 bereits regnet, dann warte bis nach 6:00“). Wer genau weiß, dass er zwischen 5:00 und 6:00 unterwegs ist, sollte sich aber auf jeden Fall einen Regenschirm mitnehmen.
Das Ausmaß der Korrelation der einzelnen Wettereignisse dürfte stark variieren, sodass man anhand der gegebenen Wahrscheinlichkeiten keinerlei feste rechnerische Verkknüpfung zwischen den untertätigen und ganztägigen Niederschlagsmengen ableiten kann.
Lest auch auf auf unserem Schwesternblog „Insight Things“ über das Thema Regenrisiko.

 (4 Stimmen, Durchnschnitt: 4,25 von 5)
(4 Stimmen, Durchnschnitt: 4,25 von 5)






Schreibe einen Kommentar