Netzwerk der Korrelationen zwischen Aktien

Wie sehen die Beziehung zwischen Aktien aus? Welche bewegen sich zusammen und welche gegensätzlich? Diese und andere Fragen werden wir im vorliegenden Beitrag hoffentlich beantworten können. Ziel ist es relevante Korrelationen zwischen Wertpapieren in einem Netzwerk-Graphen darzustellen. Dies geschieht auf Basis der XETRA-Daten welche sich mittels Stock Data Downloader herunterladen lassen. Ihr könnt einen analogen Beitrag für die NYSE hier finden.

Auszug aus dem Korrelationsnetzwerk XETRAs

Ein wenig Theorie zur Korrelation

Was passiert also, wenn man WertpapierKurse „miteinander korrelieren“ möchte? Ganz einfach: Man wählt einen Referenzkurs und ein zu korrelierenden Kurs. Zu jedem Zeitpunkt liegt dann ein Wertpapierpreis für jeden Kurs vor. Diese lassen sich gegeneinander in einen Scatterplot eintragen (siehe in der Grafik unten links).

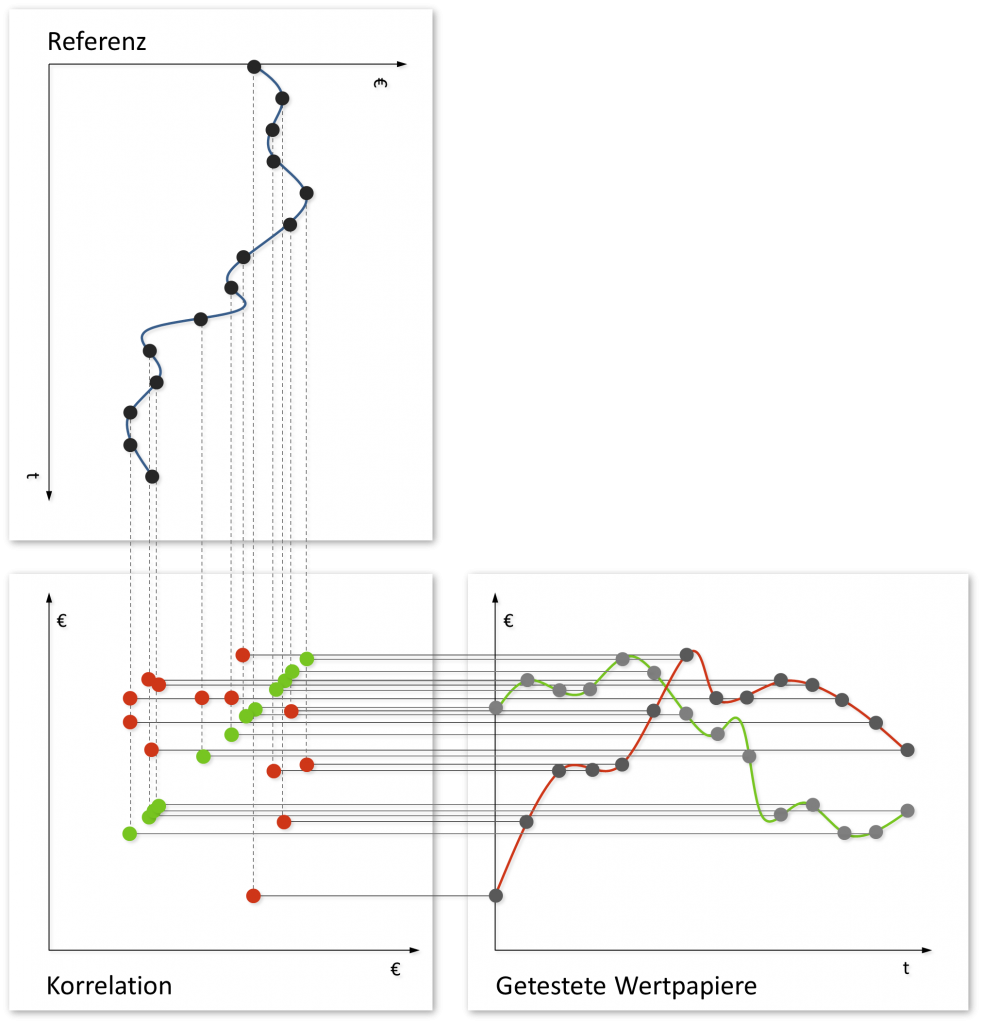
Scatterplot von Wertpapierkursen gegeneinander; je enger die Datenpunkte an einer Linie liegen desto größer die lineare Korrelation (grün korreliert perfekt, rot korreliert kaum)

Liegen dieWertepaare im Scatterplot eng entlang einer Geraden, dann ist von einer großen lineare Korrelation (Pearsonscher Korrelationskoeffizient) auszugehen. Es existieren weitere Korrelationsmaße wie beispielsweise der Rangkorrelationskoeffizient, welchen wir aber hier nicht verwenden wollen.

Datenverarbeitung

Wenden wir uns nun der Frage zu, wie man möglichst viele Korrelationskoeffizienten in einem Netzwerk-Graph zusammenführt. Dabei soll es nicht so sehr um Details als vielmehr ein grundlegendes Verständnis des Vorgangs gehen.

Die Korrelation wurden auf Basis der Daten von 2007 bis 2017, welche sich dank Stock Data Downloader ergeben, mittels R generiert. Das dplyr-Package war dabei eine große Hilfe, da es komplexe Datentransformationen stark vereinfacht.

Die Liste der Korrelationen zwischen den Aktien der XETRA ist zum Plotten jedoch nicht nicht geeignet, da wir sonst 300² Verbindungen auftragen müssten. Statt nun den Walf vor lauter Bäumen nicht zu sehen, berücksichtigen wir nur starke Korrelationskoeffizienten (d. h. kleiner als -0.9 und größer als 0.9).

Leider führen globale Ereignisse wie die Finanzkrise 2008 dazu, dass sich viele Kurse ähneln. Aus diesem Grund schließen wir Wertpapiere, welche mehr als 8 Verbindungen hätten aus. Dies führt einerseits dazu, dass Scheinkorrelationen zu einem gewissen Grad entfernt werden. Allerdings gehen dabei sicher auch einige echte Korrelationen verloren. Wir sollten das spätere Ergebnis daher weiterhin nur als Ausschnitt der Realität betrachten.

Im letzen Schritt müssen die Knoten und Verbindungen aus dem R-Skript in separate Files exportiert und in Gephi importiert werden.

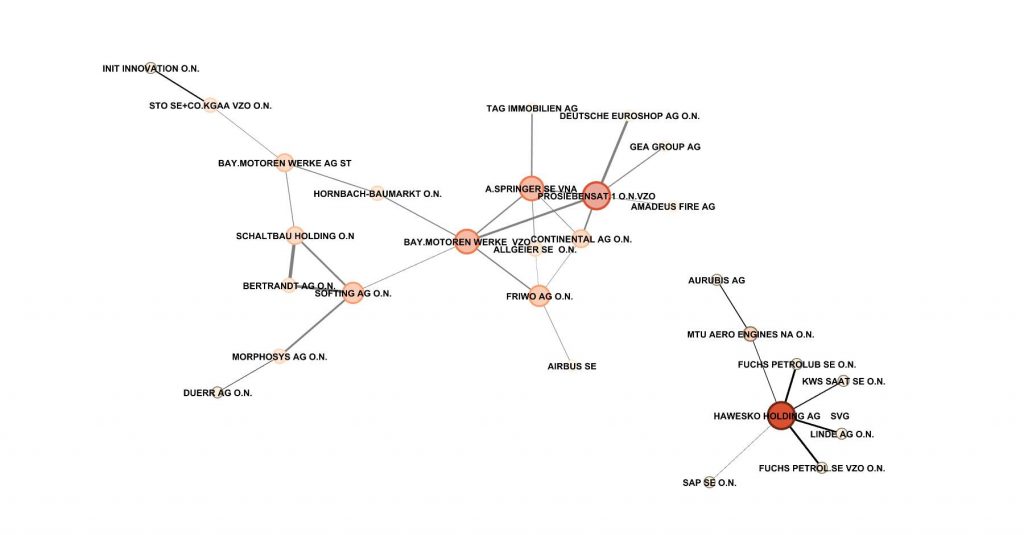
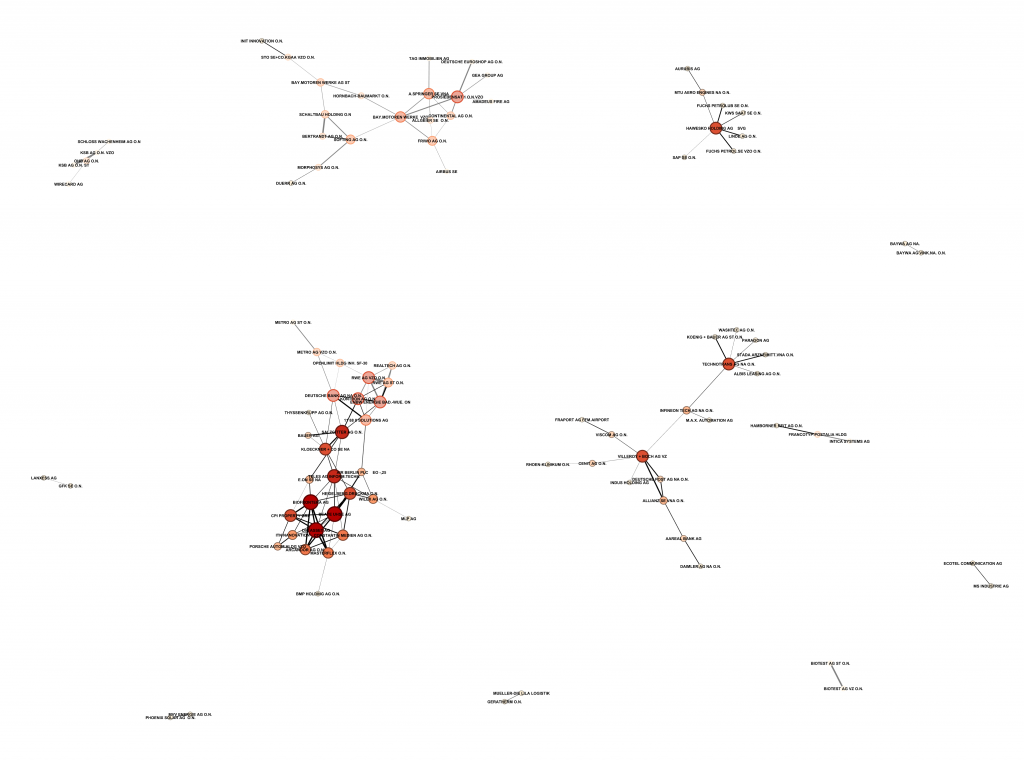
Resultierendes Netzwerk der Beziehungen

Wer sich das Gephi-Projekt mit den genauen Korrelationen herunterladen möchte, kann dies hier tun. Für alle anderen reicht sicher auch die graphische Variante unten. Große, rote Knoten deuten auf viele Verbindungen zu anderen Knoten hin. Dicke Kanten (Verbindungen) zwischen Knoten deuten auf eine starke Korrelation hin.

Netzwerk besonders nennenswerter Korrelation innerhalb von XETRA

Interessanterweise bilden sich einige „Inseln“. Ihre Untersuchung erscheint sinnvoll, steht jedoch nicht im Mittelpunkt dieses Beitrags. Stattdessen sollte jeder selbst überlegen, welchen Nutzen er aus den hier präsentierten Informationen ziehen kann.