Das Zwei-Zettel-Spiel

Früher hatten die Menschen wohl noch Zeit, um sich den wirklich interessanten Fragen des Alltags zu stellen. Thomas M. Cover stieß beispielsweise auf das Phänomen des Zwei-Zettel-Spieles. Die Idee ist simpel: Man nehme zwei Zettel und lasse von einer Person zwei zufällige (und sinnvollerweise auch unterschiedliche) Zahlen darauf schreiben. Nun darf man einen der beiden Zettel wählen. Nach Betrachtung der darauf notierten Zahl, muss man einen Tipp darüber abgeben, ob die Zahl auf dem anderen Zettel größer oder kleiner ist. Da es sich um beliebige Zahlen handeln kann, müsste die Wahrscheinlichkeit für einen korrekten Tipp bei 50% liegen. Tatsächlich gibt es aber eine Strategie, die mindestens 50% Trefferwahrscheinlichkeit erzielt. Es gibt Dinge, die sind schon verblüffend!

Die Lösungsstrategie

Die Lösungsstrategie lautet in etwa wie folgt: Denke dir eine Zufallszahl aus. Wenn die Zahl auf dem ersten Zettel kleiner ist als deine Zufallszahl, dann tippe darauf, dass die Zahl auf dem zweiten Zettel größer sein wird als die erste Zahl . Ist die Zahl auf dem ersten Zettel hingegen größer als deine Zufallszahl , dann tippe entsprechend darauf, dass die Zahl auf dem zweiten Zettel kleiner ist als die auf dem ersten Zettel .

Der Beleg

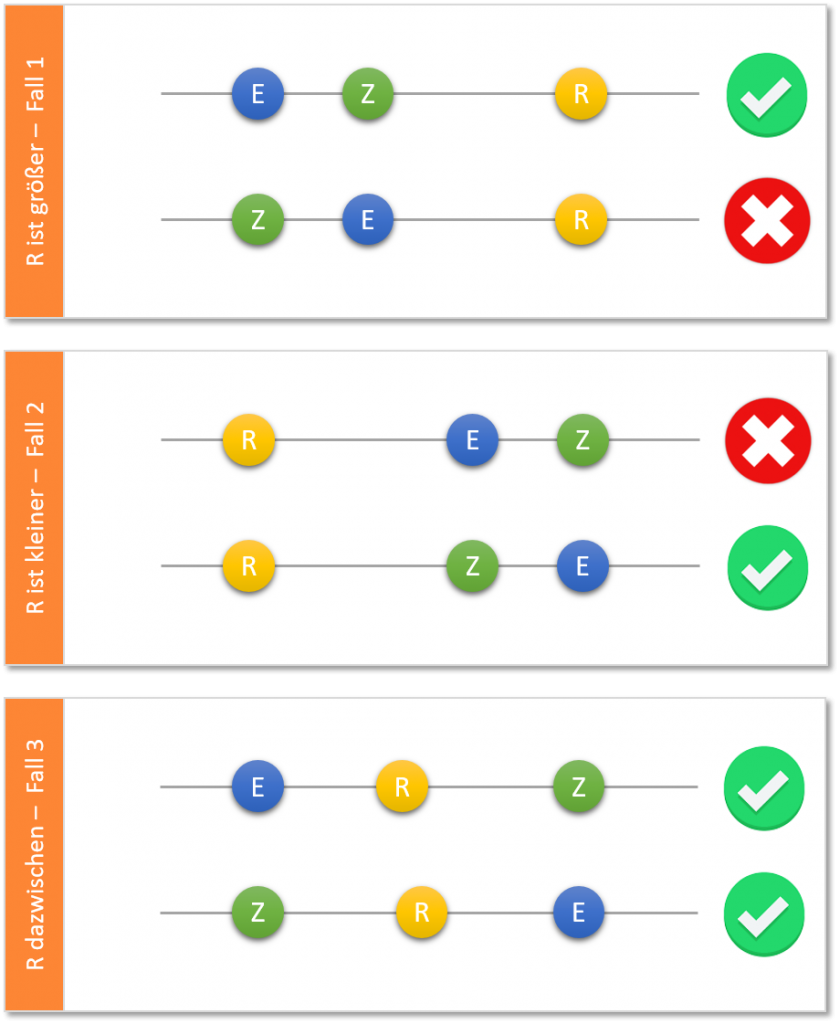
Wie beweist man das? Der einfachste Weg besteht darin, die drei möglichen Fälle zu betrachten. Im ersten Fall ist die ausgedachte Zufallszahl größer als die beiden Zahlen auf den Zetteln. Ist die zweite Zahl größer als die erste Zahl , so liegen wir richtig – sonst nicht. Im ersten Fall sehen wir uns also einer 50:50-Chance gegenüber. Gleiches gilt für den zweiten Fall. Bevor wir zum dritten (und entscheidenten) Fall kommen, gibt es hier eine kleine Übersicht:

Übersicht der einzelnen Fälle

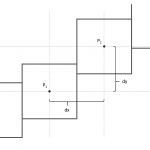
Augenscheinlich kann man im dritten Fall nicht falsch liegen. Seien P₁, P₂, P₃ die Wahrscheinlichkeiten, dass die Fälle 1, 2 oder 3 eintreten. Weil P₁+P₂+P₃=1 können wir die Wahrscheinlichkeit eines Erfolges P_E mathematisch wie folgt modellieren.

Die Erfolgswahrscheinlichkeit beträgt also 50% zzgl. der Wahrscheinlichkeit, dass Fall 3 eintritt. Folglich weist die Strategie eine Erfolgswahrscheinlichkeit von mehr als 50% auf!

Bedeutung und Ausblick

Revolutionär am Zwei-Zettel-Spiel ist aus meiner Sicht die Universalität! Es ist vollkommen egal, wie und verteilt sind. Und selbst wenn man extrem ungünstig wählt, ist man noch immer nicht schlechter als mit blindem Raten. Für mich rangiert das Zwei-Zettel-Spiel in der Liga, in der auch die Tschebyscheff-Ungleichung zu Hause ist. Wie auch die Strategie des Zwei-Zettel-Spieles erscheint die Ungleichung sinnlos, wenn man mehr Informationen über die Verteilung der Zufallsvariable besitzt. Hat man diese Informationen aber nicht, dann kann die Formel Gold wert sein!